
2. 能通过对样本的频率分布估计总体分布;
1. 能运用简单随机抽样、分层抽样的方法抽取样本;
3. 数据 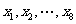 平均数为6,标准差为2,则数据
平均数为6,标准差为2,则数据 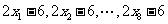 的平均数为 ,方差为 .
的平均数为 ,方差为 .
2.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A.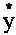 =1.23x+4 B.
=1.23x+4 B.  =1.23x+5
=1.23x+5
C. 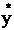 =1.23x+0.08 D.
=1.23x+0.08 D.  =0.08x+1.23
=0.08x+1.23
1.下列说法中,正确的是( )
A.频率分布直方图中各小长方形的面积不等于相应各组的频率
B.一组数据的标准差是这组数据的方差的平方
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
3. 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示:
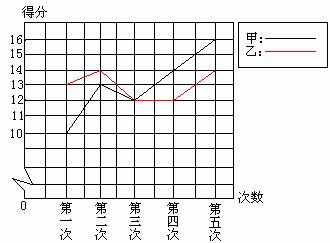
则甲得分的方差为__________,乙得分的方差为____________.从而你得出的结论是______________________.
[经典范例]
例1 某风景区对5个旅游景点的门票价格进行了调整,据统计,调整前后各景点的游客人数基本不变,有关数据如下表所示:
|
景点 |
A |
B |
C |
D |
E |
|
原价(元) |
10 |
10 |
15 |
20 |
25 |
|
现价(元) |
5 |
5 |
15 |
25 |
30 |
|
平均日人数(千人) |
1 |
1 |
2 |
3 |
2 |
(1) 该景区称调整前后这5个景点门票的平均收费不变,平均总收入持平,问风景区是怎样计算的?
(2) 另一方面,游客认为调价后风景区的平均日收入相对于调价前,实际上增加了9.4%,问游客是怎样计算的?
(3) 你认为风景区和游客哪一方的说法能反映整体实际?
解:
例2 某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上,每隔30分抽一包样品,称其质量是否合格,分别记录抽查数据如下:
甲车间:102,101,99,103,98,99,98;
乙车间:110,115,90,85,75,115,110.
(1) 这种抽样方法是何种抽样方法?
(2) 估计甲、乙两车间产品重量的均值和方差,并说明哪个车间产品较稳定?
解:
例3 在某次有奖销售中,每10万份奖券中有一个头奖(奖金10000元) ,2个二等奖(奖金5000元),500个三等奖(奖金100元),10000个四等奖(奖金5元) .试求每张奖券平均获利多少?(假设所有奖券全部卖完,每张奖券面值3元.)
解:
例4 给出施化肥量对水稻产量影响的试验数据:
|
施化肥量x |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
水稻产量y |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
(1)画出上表的散点图;(2)求出回归直线.
解:(完成解答)
(1)散点图:
(2)表中的数据进行具体计算,列成以下表格
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
xi |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
yi |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
|
xiyi |
4950 |
6900 |
9125 |
12150 |
15575 |
18000 |
20475 |
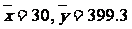 , ,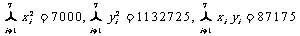 |
故可得到:
从而得回归直线方程是:
[追踪训练]
2. 已知样本99,100,101,x,y的平均数是100,方差是2,则xy=____________
1.已知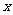 ,
,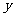 之间的一组数据:
之间的一组数据:
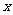 |
0 |
1 |
2 |
3 |
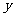 |
1 |
3 |
5 |
7 |
则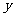 与
与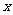 的线性回归方程
的线性回归方程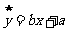 必过 ( )
必过 ( )
A.(2,2)点 B.(1.5,0)点 C.(1,2)点 D.(1.5,4)点
1、以下是收集到的新房屋销售价格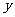 与房屋的大小
与房屋的大小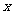 的数据:
的数据:
房屋大小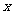 ( (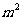 ) ) |
80 |
105 |
110 |
115 |
135 |
销售价格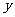 (万元) (万元) |
18.4 |
22 |
21.6 |
24.8 |
29.2 |
(1)画出数据的散点图;(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线.
[解]
3. 求线性回归方程的步骤:

(4)将上述有关结果代入公式,求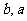 ,写出回归直线方程.
,写出回归直线方程.
[经典范例]
例1一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:
|
x |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
y |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
(1)画出散点图;(2)求月总成本y与月产量x之间的回归直线方程.
[解]
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
xi |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
yi |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
|
xiyi |
2.43 |
2.264 |
2.856 |
3.264 |
3.590 |
4.07 |
4.643 |
5.090 |
5.652 |
6.096 |
6.653 |
7.245 |
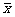 = =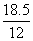 , ,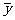 = =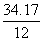 =2.8475, =2.8475, =29.808, =29.808, =99.2081, =99.2081, =54.243 =54.243 |
1)画出散点图:
2)设回归直线方程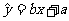 ,
,
例2 已知10只狗的血球体积及红血球数的测量值如下:
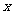 |
45 |
42 |
46 |
48 |
42 |
35 |
58 |
40 |
39 |
50 |
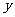 |
6.53 |
6.30 |
9.52 |
7.50 |
6.99 |
5.90 |
9.49 |
6.20 |
6.59 |
8.72 |
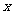 (血球体积
(血球体积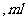 ),
),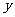 (红血球数,百万)
(红血球数,百万)
(1)画出上表的散点图;(2)求出回归直线度且画出图形.
[解]
追踪训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com