
3.能识别简单的流程图所描述的算法
2.能用流程图表示顺序结构
1.了解常用流程图符号(输入、输出框,处理,判断,起止框,流程线等)的意义
3. 已知某工厂工人某天加工的零件个数的茎叶图如右图所示,(以零件个数的前两位为茎,后一位为叶),那么工人生产零件的平均个数及生产的零件个数超过130的比例分别是( )
A. 116.5与13.3% B. 120.5与10%
C. 120.5与13.3% D. 126.5与10%
2.经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多 人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的
人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的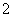 位“喜欢”摄影的同学、
位“喜欢”摄影的同学、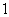 位“不喜欢”摄影的同学和
位“不喜欢”摄影的同学和 位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人.
位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人.
|
10 11 12 13 |
78 02223666778 0012234466788 0234 |
1.把一个容量为100的样本分成若干组,已知某组的频率为0.3,那么该组的频数为________
3.对甲、乙两所学校2005年的高考数学成绩进行统计分析,得到的样本的平均分为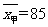 ,
, ,样本的方差为
,样本的方差为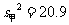 ,
,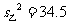 ,由此可知两校考生中成绩较为均衡的是 校.
,由此可知两校考生中成绩较为均衡的是 校.
[经典范例]
例1 某单位有职工160人,其中业务人员96人,管理人员40人,后勤服务人员24人,为了了解职工的某种情况,要从中抽取一个容量为20的样本.试用三种方法分别解答.
解:
例2 从高三学生中抽取50名同学参加知识竞赛,成绩分组及各组的频数如下:(单位:分)[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100),8
(1)列出样本频率分布表(含累积频率);
(2)画出频率分布直方图;
(3)估计成绩在[60,90)内学生的频率;
解:
例3 为检查一批钢筋抗拉强度,抽样得到该指标的一个容量为20的样本:
110,120,120,125,125,125,125,130,135,135,
100,115,120,125,125,125,125,130,145,145.
(1)计算平均抗拉强度系数和标准差;
(2)估计这批钢筋有多少落入平均数与2倍标准差的范围内.
解:
例4 一台机器由于使用时间较长,生产的零件有一些会有缺损.按不同转速生产出来的零件有缺损的统计数据如下:
转速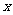 (转/s) (转/s) |
16 |
14 |
12 |
8 |
每小时生产有缺损零件数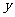 (件) (件) |
11 |
9 |
8 |
5 |
(1)作出散点图;
(2)如果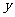 与
与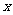 线性相关,求线性回归方程;
线性相关,求线性回归方程;
(3) 如果实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器运转速度应控制在什么范围内?
解:
[追踪训练]
2.一个容量为20的样本数据,分组后组据与频数如下:
[10,20),2;[20,30),3;[30,40),4;[40,50),5;[50,60),4;[60,70),2.则样本在区间 上的频率为(
)
上的频率为(
)
A.5% B.25% C.50% D.70%
1.为了保证分层抽样时,每个个体等可能抽取,必须( )
A.每层的个体数相等
B.每层中抽的个体数相等
C.不同的层中,每个个体被抽到的可能性不相等
D.每层等可能抽取的样本个数可能一样,也可能不一样,但每层被抽取的个体数与这一层中个体数的比等于样本容量与总体个数的比
3. 培养学生动手能力和解决实际问题能力.
课堂互动]
[经典范例]
例某中学高中部共有16个班级,其中高一年级6个班,高二年级6个班,高三年级4个班.每个班的人数均在46人左右(44人-49人),各班的男女学生数均基本各占一半.现要调查这所学校学生的周体育活动时间,它是指学生在一周中参加早锻炼、课间操、课外体育活动、体育比赛等时间的总和(体育课、上学和放学路上的活动时间不计在内).为使所得数据更加可靠,应在所定抽样的“周”之后的两天内完成抽样工作. 此外还有以下具体要求:
(1)分别对男、女学生抽取一个容量相同的样本,样本容量可在40-50之间选择.
(2)写出实习报告,其中含:全部样本数据;相应于男生样本的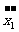 与
与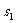 ,相应于女生的
,相应于女生的 与
与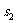 ,相应于男、女全体的样本的
,相应于男、女全体的样本的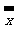 ;对上面计算结果作出分析.
;对上面计算结果作出分析.
[解](1)由于各个年级的学生参加体育活动的时间存在差异,应采用分层抽样;又由于各班的学生数相差不多,且每班的男女学生人数也基本各占一半,为便于操作,分层抽样时可以班级为单位.关于抽取人数,如果从每班中抽取男、女学生各3人,样本容量各为48(3×16),符合对样本容量的要求.
(2)实习报告如表所示:
|
题目 |
调查本校学生周体育活动的时间 |
||
|
对抽取样本的要求 |
1.周体育活动时间,指一周中(包括双休日)参加早锻炼、课间操、课外体育活动、体育比赛等时间的总和(体育课和上学、放学路上的活动时间不计在内). 2.在所定抽样的“周”之后的两天内完成抽样工作. 3.男、女学生的两个样本的容量相同,并在40-50之间选择. |
||
|
确定抽样方法和样本容量 |
采用分层抽样,以班为单位,从每班中抽取男、女学生各3人,两个样本的容量均为48,在各班抽取时,采用随机数表法. |
||
|
样本数据(单位:分) |
|
男生 |
女生 |
|
一年级 |
380 500 245 450 145 620 480 420 520 280 550 660 350 500 330 600 180 520 |
230 460 600 110 420 105 580 400 420 380 180 500 140 450 600 400 125 540 |
|
|
二年级 |
420 580 510 175 280 630 400 150 450 360 450 330 400 420 300 500 580 400 |
280 380 530 95 100 570 300 220 320 250 300 350 400 360 130 450 590 230 |
|
|
三年级 |
380 420 235 125 400 470 330 200 420 280 300 410 |
200 460 165 400 75 430 300 220 250 130 270 340 |
|
|
计算结果 |
男生 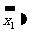 , , 女生 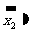 , ,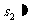 男、女生全体  |
||
|
计算结果分析 |
从计算结果看到,在周体育活动时间方面,可以估计男生比女生略多,且波动程度略小,这所学校高中学生的周体育活动时间平均约为 分. |
追踪训练
在本班范围内,就每名学生所在家庭的月人均用水量进行调查.调查的具体要求是:先查得在同一月份内各家的用水量(单位以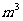 计),然后将它除以家庭人中数(结果保留到小数点后第2位);再将所得数据进行整理、计算和分析,完成下列实习报告.
计),然后将它除以家庭人中数(结果保留到小数点后第2位);再将所得数据进行整理、计算和分析,完成下列实习报告. 
|
题目 |
调查本班每名学生所在家庭的月人均用水量 |
|
对获取数据的要求 |
这里的用水量是指同一月份内各学生所在家庭的人均用水量(下月第1天的水表数与本月第1天的水表数之差),数据单位为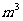 ,结果保留到小数点后第2位. ,结果保留到小数点后第2位. |
|
样本数据 (单位: 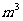 ) ) |
|
|
频率分布表 |
|
|
频率分布直方图 |
|
|
样本平均数 |
|
|
统计结果的分析 |
要求讨论:通过对本问题的调查统计分析,可对全班同学所在地区的家庭月人均用水量作出何种估计? |
|
备注 |
1.为了在所要求的时间内获取数据,调查任务就提前布置. 2.实习报告可由部分同学完成,然后向全班同学报告并进行讨论. |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com