1．体会分层抽样的的概念及如何用分层抽样获取样本；

4. 要从1003名学生中选取一个容量为20的样本，试叙述系统抽样的步骤。

[解]

第一步　 将1003名学生有随机方式进行编号；

第二步　 从总体中剔除3人(剔除方法可用随机数表法)，将剩下的1000名学生重新编号并分成20段;

第三步　 在第一段000、001、002、003、…、049这十个编号中用简单随机抽样确定起始号码，比如013

第四步　 将013逐次加上部分的“长度”(第一部分中个体的个数)的0倍、1倍、2倍、…、19倍得到样本:013、063、113、163、…963.

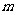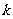3．一个总体中有100个个体，随机编号为0,1,2, ．．．，99,依编号顺序平均分成10个小组，组号依次为1,2,3, ．．．,10．现用系统抽样的方法抽取一个容量为10的样本，规定如果在第一组随机抽取的号码为，那么在第组中抽取的号码个位数字与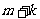的个位数字相同．若，则在第7组中抽取的号码是______63_______．

2．全班有50位同学，需要从中选取7人，若采用系统抽样的方法来选取，则每位同学能被选取的可能性是

1．为了了解参加一次知识竞赛的1 252名学生的成绩，决定采用系统抽样的方法抽取一个容量为50的样本，那么总体中应随机剔除个体的数目是　　　　(　A　)

(A)2　　　(B)3　　　

(C)4　　　(D)5

1.系统抽样

　系统抽样的概念: 将总体平均分成几个部分，然后按照一定的规则，从每个部分中抽取一个个体作为样本，这样的抽样方法称为系统抽样(systematic sampling)

系统抽样的步骤为：

(1)采用随机的方式将总体中的个体编号;

(2)将整个的编号按一定的间隔(设为k)分段，当N/n (N为总体中的个体数，n为样本容量)是整数时，k=N/n；当N/n不是整数时，从总体中剔除一些个体 ，使剩下的总体中个体的个数N^’能被n整除，这时，k=N^’/n并将剩下的总体重新编号;

(3)在第一段中用简单随机抽样确定起始的个体编号L;

(4)将编号为L，L+k,L+2k,…,L+(n-1)k的个体抽出.

[小结]系统抽样是以简单随机抽样为基础的一种抽样方法，对于容量较大、个体差异不明显的总体通常采用这种抽样方法，在保证公平客观的前提下简化抽样过程．在用系统抽样方法抽取样本时，如果总体个数不能被样本容量整除，可以从总体中剔除一些个体，使剩下的总体中的个体的个数能被样本容量整除.

[经典范例]

例1　 在1 000个有机会中奖的号码(编号为000-999)中，在公证部门监督下随机抽取的方法确定后两位数为88的号码为中奖号码，这是运用哪种抽样方法来确定中奖号码的？依次写出这10个中奖号码？

[解]

本题中是运用了系统抽样的方法来确定中奖号码的，中奖号码依次为：088,188,288,388,488,588,688,788,888,988

例2　 某单位在岗职工共624人，为了调查工人用于上班途中的时间，决定抽取10%的工人进行调查．试采用系统抽样方法抽取所需的样本.

[分析]　 因为624的10%约为62，624不能被62整除，为了保证“等距”分段，应剔除4人．

[解]　 第一步　 将624名职工用随机方式进行编号；

第二步　 从总体中剔除4人(剔除方法可用随机数表法)，将剩下的620名职工重新编号(分别为000，001，002，……，619)，并分成62段；

第三步　 在第一段000，……，009这十个编号中用简单随机抽样确定起始号码i₀;

第四步　 将编号为i₀，i₀+10，……，i₀+610的个体抽出，组成样本．

例3　 某制罐厂每小时生产易拉罐10 000个，每天生产时间为12h，为了保证产品的合格率，每隔一段时间要抽取一个易拉罐送检，工厂规定每天共抽取1 200个进行检测，请你设计一个抽样方案。　

[解]

每天共生产易拉罐120 000个，共抽取1200个，所以分1200组，每组100个，然后采用简单随机抽样法从001-100中随机选出一个编号，例如选出的是013号，则从第13个易拉罐开始，每隔100个，拿出一个送检，或者根据每小时生产10 000个，每隔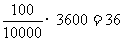s拿出一个易拉罐送检。

例4　 现要从999名报名者中随机选取100名参加某活动，请你用系统抽样法设计一种方案，叙述其步骤。你能找到另外的抽样方案吗？比较两种方案的合理性和易操作性

[解]按系统抽样法，因为100不能整除999，所以首先将999人编号，采用随机数表法剔除99名，再将剩下的900名报名者重新编号001-900，从001号顺次下去每9人一组，等分成100组，利用抽签法或随机数表法，从1-9个数中随机选出一个数，新编号为该数字加上9的倍数的报名者入选。例如选出的随机数为3，则新编号为003,012,021，…，894共100人入选。

还可以采取以下抽样方法：首先将999名报名者编号为001-999，因为111可以整除999，将这999个编号从001开始顺次每9个一组，然后选用简单随机抽样法从1-9的9个数字中随机地抽出一个数字，编号为该数字加上9的倍数的共111名报名者先挑选出来，例如：随机抽到的是7，则编号为007,016,025，…,988,997共111名，最后，再利用随机数表从111名中随机抽取11名剔除。

点评：此方法较之系统抽样法更易操作，因为虽然999不能被100整除，但余数99非常大，接近于除数100，而且采用随机数表法从999个数字中随机抽出 99个数剔除的工作量也较大。后一种方法先通过系统抽样，随机抽取111名，再利用随机数表法，从111个数字中随机抽出11个来剔除，操作起来要相对方便得多。

追踪训练

2．感受系统抽样也是等可能性抽样，是否需要用系统抽样，主要是看总体个数的多少.

[课堂互动]

自学评价

案例1 　某校高一年级有20个班，每班有50名学生．为了了解高一学生的视力状况，从这1000人中抽取一个容量为100的样本进行检查，应该怎样抽样?

[分析]

这个案例的总体中个体数较多，生活中还有容量大的多的总体，面对这样的总体，采用抽签或随机数表等简单随机抽样方法是不科学的．抽取样本最关键的就是要保证抽样过程的公平性，要保证总体中每个个体被抽到的机会均等．在这样的前提下，我们可以寻求更好的抽样方法．

系统抽样以简单随机抽样为基础，通过将较大容量的总体分组，只需在某一个组内用简单随机抽样方式来获取一个个体，然后在一定规则下就能抽取出全部样本.

1．体会系统抽样的的概念及如何用系统抽样获取样本；

4.为了分析某次考试情况，需要从2 000份试卷中抽取100份作为样本，如何用随机数表法进行抽取？

[解]

第一步，将所有试卷编号 ：0000,0001,0002，…,1998,1999。　　　　　　　　　

第二步，选定随机数表中第一个数1作为开始。

第三步，从选定的数1开始按四个数字一组向右读下去，一行读完时按下一行自左向右继续读，将超过1999或重复的四位数去掉，保留下来的四位数直到取足100个为止。

3.从100件电子产品中抽取一个容量为25的样本进行检测，试用随机数表法抽取样本。

[解]

第一步，将所有电子产品编号 ：00,01,02，…,98,99。　　　　　　　　　

第二步，选定随机数表中第一个数1作为开始。

第三步，从选定的数1开始按二个数字一组向右读下去，一行读完时按下一行自左向右继续读，将重复的二位数去掉，保留下来的二位数直到取足25个为止。