
6.2 总体分布的估计
第19课时 频率分布表
[学习导航]
学习要求
4.某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
|
人数 |
管理 |
技术开发 |
营销 |
生产 |
小计 |
|
老年 |
40 |
40 |
40 |
80 |
200 |
|
中年 |
80 |
120 |
160 |
240 |
600 |
|
青年 |
40 |
160 |
280 |
720 |
1200 |
|
小计 |
160 |
320 |
480 |
1040 |
2000 |
(1)若要抽取40人调查身体情况,则应该怎样抽样?(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?(3)若要抽20人调查对北京奥运会筹备情况的了解,则应怎样抽样?
[解]
(1)因为身体状况主要与年龄有关,所以应按老年、中年、青年分层抽样法进行抽样,要抽取40人,可以在老年、中年、青年职工中分别抽取4,12,24人.
(2)因为出席这样的座谈会的人员应该代表各个部门,所以可用按部门分层抽样的方法进行抽样.要抽取25人,可以在管理、技术开发、营销、生产各部门的职工中分别随机抽取2,4,6,13人.
(3)对北京奥运会筹备情况的了解与年龄、部门关系不大,可以用系统抽样或简单随机抽样进行.
03、13、23、33、43
(2) 因为总体由两类差异明显的个体构成,所以应采用分层抽样的方法进行抽取:其中男生抽三名,女生抽两名。
3.某班有50名学生,(其中有30名男生,20名女生)现调查平均身高,准备抽取10%,问应如何抽样?如果已知男女身高有显著不同,又应如何抽样?
解:(1)可用系统抽样的方法:
第一步 先将这50名学生从00到49随机编号,并分成5段;
第二步 在第一段00、01、02、03、…、09这十个编号中用简单随机抽样确定起始号码,比如03
第三步 将003逐次加上部分的“长度”(第一部分中个体的个数)的0倍、1倍、2倍、…、9倍得到样本:
2.某商场想通过检查发票及销售记录的2%来快速估计每月的销售总额,采取如下方法:从某本50张的发票存根中随机抽取一张,如15号,然后按顺序往后将65号、115号、165号、…发票上的销售额组成一个调查样本。这种抽取样本的方法是 ( B )
(A)抽签法 (B)系统抽样
(C)分层抽样 (D)随机数表法
1.某公司生产三种型号的轿车,产量分别为1200辆、6000辆、2000辆。为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车应分别抽取__6_____、___30___和____10__辆。
2.三种抽样方法的比较
|
类别 |
特点 |
相互联系 |
适用范围 |
共同点 |
|
简单随机抽样 |
从总体中逐个抽取 |
|
总体中的个体数较少 |
抽样过程中每个个体被抽到的可能性相同 |
|
系统抽样 |
将总体平均分成几部分,按事先确定的规则分别在各部分中抽取 |
在起始部分抽样时,采用简单随机抽样 |
总体中的个体数较多 |
|
|
分层抽样 |
将总体分成几层,按各层个体数之比抽取 |
各层抽样时采用简单随机抽样或系统抽样 |
总体由差异明显的几部分组成 |
[精典范例]
例1 某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,工人20人,上级机关为了了解政府机构改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,请具体实施抽取。
[解]
因为机构改革关系到各种人的不同利益,故采用分层抽样方法为妥。

所以从副处以上干部中抽取2人,从一般干部中抽取14人,从工作中抽取4人。
例2 某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如下表所示:
|
很喜爱 |
喜爱 |
一般 |
不喜爱 |
|
2435 |
4567 |
3926 |
1072 |
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
分析:因为总体中人数较多,所以不宜采用简单随机抽样,又由于持不同态度的人数差异较大,故也不宜用系统抽样方法,而以分层抽样为妥。
[解]
可用分层抽样方法,其总体容量为12000,
“很喜爱”占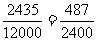 ,应取
,应取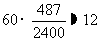 人
人
“喜爱” 占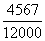 ,应取
,应取 人
人
“一般” 占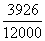 ,应取
,应取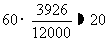 人
人
“不喜爱”占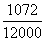 ,应取
,应取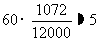 人
人
因此,采用分层抽样的方法在“很喜爱”、“喜爱”、“一般”和“不喜爱”的2435人、4567人、3926人和1072人中分别抽取12人、23人、20人和5人。
例3 某所学校有小学部、初中部和高中部,在校小学生、初中生和高中生之比为5:2:3,且已知初中生有800人,现要从这所学校中抽取一个容量为80的样本以了解他们对某一问题的看法,应采用什么抽样方法?从小学部、初中部及高中部各抽取多少名?总体上看,平均多少名学生中抽取到一名学生?
[解]
因为总体由三类差异明显的个体构成,所以应采用分层抽样的方法进行抽取。
由于样本容量为80,小学生、初中生、高中生之比为5:2:3,
所以就抽取
小学生为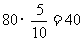 (人),
(人),
初中生为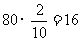 (人)
(人)
高中生为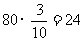 (人)
(人)
800名初中生抽取16人, ,所以平均50名学生中抽取一名学生。
,所以平均50名学生中抽取一名学生。
例4 下列问题中,采用怎样的抽样方法较为合理?
(1)从10台冰箱中抽取3台进行质量检查;
(2)某电影院有32排座位,每排有40个座位,座位号为1-40。有一次报告会坐满了听众,报告会结束以后为听取意见,需留下32名听众进行座谈;
(3)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
分析:(1)用抽签法或随机数表法。
(2)总体容量比较大,用抽签法或随机数表法比较麻烦。由于人员没有明显差异,且刚好32排,每排人数相同,可用系统抽样。
(3)由于学校各类人员对这一问题的看法可能差异较大,故应采用分层抽样方法。
[解]
(1) 用抽签法或随机数表法。
(2)将每排的40个人组成一组,共32组,从第一排至第32排分别为第1-32组,先在第一排用简单随机抽样法抽出一名听众,再将其各排与此听众座位号相同的听众全部取出。
(3)总体容量为160,故样本中
教师人数应为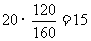 名,
名,
行政人员人数为
后勤人员人数为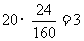
追踪训练一
1.分层抽样
分层抽样的概念:当总体由差异明显的几个部分组成时,为了使样本更客观地反映总体情况,我们常常将总体中的个体按不同的特点分成层次比较分明的几部分,然后按各部分在总体中所占的比实施抽样,这样的抽样方法称为分层抽样(stratified sampling)
分层抽样的步骤为:
(1)将总体按一定标准分层;
(2)计算各层的个体数与总体的个体数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(4)在每一层进行抽样(可用简单随机抽样或系统抽样)。
[小结]①分层抽样适用于总体由差异比较明显的几个部分组成的情况,是等可能抽样,它也是客观的、公平的;
②分层抽样是建立在简单随机抽样或系统抽样的基础上的,由于它充分利用了已知信息,使样本具有较好的代表性,而且在各层抽样时可以根据情况采用不同的抽样方法,因此在实践中有着非常广泛的应用.
3.简单随机抽样、系统抽样、分层抽样的特点及适用范围。
[课堂互动]
自学评价
案例1 某校高一、高二和高三年级分别有学生1000,800和700名,为了了解全校学生的视力情况,欲从中抽取容量为100的样本,怎样抽样较为合理.
[分析]如果在2500名学生中随机抽取100名学生作为样本,或者在三个年级中平均抽取学生组成样本,这样的样本是否合理?能否反映总体情况?
由于不同年级的学生视力状况有一定的差异,为准确反映客观实际,不仅要使每个个体被抽到的机会均等,而且要注意总体中个体的层次性,从而使抽取的样本具有良好的代表性. 对于这种容量较大、个体差异较大且明显分成几部分的总体,就考虑用分层抽样来抽取样本.
2.感受分层抽样也是等可能性抽样,它适用于总体由差异明显的几部分组成的;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com