
1. 在本班范围内,就每名学生所在家庭的月人均用水量进行调查.调查的具体要求是:先查得在同一月份内各家的用水量(单位以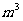 计),然后将它除以家庭人中数,结果保留到小数点后第2位);再将所得数据进行整理、计算和分析,完成下列实习报告.
计),然后将它除以家庭人中数,结果保留到小数点后第2位);再将所得数据进行整理、计算和分析,完成下列实习报告. 
|
题目 |
调查本班每名学生所在家庭的月人均用水量 |
|
对获取数据的要求 |
这里的用水量是指同一月份内各学生所在家庭的人均用水量(下月第1天的水表数与本月第1天的水表数之差),数据单位为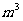 ,结果保留到小数点后第2位. ,结果保留到小数点后第2位. |
|
样本数据 (单位: 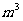 ) ) |
|
|
频率分布表 |
|
|
频率分布直方图 |
|
|
样本平均数 |
|
|
统计结果的分析 |
要求讨论:通过对本问题的调查统计分析,可对全班同学所在地区的家庭月人均用水量作出何种估计? |
|
备注 |
1.为了在所要求的时间内获取数据,调查任务就提前布置. 2.实习报告可由部分同学完成,然后向全班同学报告并进行讨论. |
3. 培养学生动手能力和解决实际问题能力.
课堂互动]
[精典范例]
例1 某中学高中部共有16个班级,其中一年级6个班,二年级6个班,三年级4个班.每个班的人数均在46人左右(44人-49人),各班的男女学生数均基本各占一半.现要调查这所学校学生的周体育活动时间,它是指学生在一周中参加早锻炼、课间操、课外体育活动、体育比赛等时间的总和(体育课、上学和放学路上的活动时间不计在内).为使所得数据更加可靠,应在所定抽样的“周”之后的两天内完成抽样工作. 此外还有以下具体要求:
(1)分别对男、女学生抽取一个容量相同的样本,样本容量可在40-50之间选择.
(2)写出实习报告,其中含:全部样本数据;相应于男生样本的 与
与 ,相应于女生的
,相应于女生的 与
与 ,相应于男、女全体的样本的
,相应于男、女全体的样本的 ;对上面计算结果作出分析.
;对上面计算结果作出分析.
[解](1)由于各个年级的学生参加体育活动的时间存在差异,应采用分层抽样;又由于各班的学生数相差不多,且每班的男女学生人数也基本各占一半,为便于操作,分层抽样时可以班级为单位.关于抽取人数,如果从每班中抽取男、女学生各3人,样本容量各为48(3×16),符合对样本容量的要求.
(2)实习报告如表所示:
|
题目 |
调查本校学生周体育活动的时间 |
||
|
对抽取样本的要求 |
1.周体育活动时间,指一周中(包括双休日)参加早锻炼、课间操、课外体育活动、体育比赛等时间的总和(体育课和上学、放学路上的活动时间不计在内). 2.在所定抽样的“周”之后的两天内完成抽样工作. 3.男、女学生的两个样本的容量相同,并在40-50之间选择. |
||
|
确定抽样方法和样本容量 |
采用分层抽样,以班为单位,从每班中抽取男、女学生各3人,两个样本的容量均为48,在各班抽取时,采用随机数表法. |
||
|
样本数据(单位:分) |
|
男生 |
女生 |
|
一年级 |
380 500 245 450 145 620 480 420 520 280 550 660 350 500 330 600 180 520 |
230 460 600 110 420 105 580 400 420 380 180 500 140 450 600 400 125 540 |
|
|
二年级 |
420 580 510 175 280 630 400 150 450 360 450 330 400 420 300 500 580 400 |
280 380 530 95 100 570 300 220 320 250 300 350 400 360 130 450 590 230 |
|
|
三年级 |
380 420 235 125 400 470 330 200 420 280 300 410 |
200 460 165 400 75 430 300 220 250 130 270 340 |
|
|
计算结果 |
男生  , , 女生  , , 男、女生全体 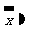 |
||
|
计算结果分析 |
从计算结果看到,在周体育活动时间方面,可以估计男生比女生略多,且波动程度略小,这所学校高中学生的周体育活动时间平均约为 分. |
追踪训练
2. 能通过对样本的频率分布估计总体分布;
1. 能运用简单随机抽样、分层抽样的方法抽取样本;
3. 数据  平均数为6,标准差为2,则数据
平均数为6,标准差为2,则数据  的平均数为 6 ,方差为 16 .
的平均数为 6 ,方差为 16 .
2.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( C )
A. =1.23x+4 B.
=1.23x+4 B.  =1.23x+5
=1.23x+5
C.  =1.23x+0.08 D.
=1.23x+0.08 D.  =0.08x+1.23
=0.08x+1.23
1.下列说法中,正确的是( D )
A.频率分布直方图中各小长方形的面积不等于相应各组的频率
B.一组数据的标准差是这组数据的方差的平方
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
3. 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示:

则甲得分的方差为_____4_____,乙得分的方差为_____0.8________.从而你得出的结论是_______乙的成绩较稳定,甲的成绩在不断提高,而乙的成绩则无明显提高._______________.
[精典范例]
例1 某风景区对5个旅游景点的门票价格进行了调整,据统计,调整前后各景点的游客人数基本不变,有关数据如下表所示:
|
景点 |
A |
B |
C |
D |
E |
|
原价(元) |
10 |
10 |
15 |
20 |
25 |
|
现价(元) |
5 |
5 |
15 |
25 |
30 |
|
平均日人数(千人) |
1 |
1 |
2 |
3 |
2 |
(1) 该景区称调整前后这5个景点门票的平均收费不变,平均总收入持平,问风景区是怎样计算的?
(2) 另一方面,游客认为调价后风景区的平均日收入相对于调价前,实际上增加了9.4%,问游客是怎样计算的?
(3) 你认为风景区和游客哪一方的说法能反映整体实际?
解: (1)风景区是这样计算的:调整前的平均价格: 元,调整后的平均价格:
元,调整后的平均价格: 元.因为调整前后的平均价格不变,平均日人数不变,所以平均日收入持平.
元.因为调整前后的平均价格不变,平均日人数不变,所以平均日收入持平.
(2)游客是这样计算的:原平均日总收入: (千元) ,现平均日总收入:
(千元) ,现平均日总收入: (千元),所以平均日总收入增加了:
(千元),所以平均日总收入增加了: .
.
(3)游客的说法较能反映整体实际.
例2 某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上,每隔30分抽一包样品,称其质量是否合格,分别记录抽查数据如下:
甲车间:102,101,99,103,98,99,98;
乙车间:110,115,90,85,75,115,110.
(1) 这种抽样方法是何种抽样方法?
(2) 估计甲、乙两车间产品重量的均值和方差,并说明哪个车间产品较稳定?
解: (1)根据系统抽样方法的定义,可知这种方法是系统抽样.
(2) ,
,
 ,
,
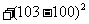
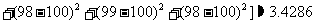 ,
,
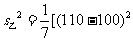
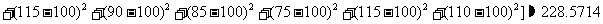 由于
由于 ,
, ,故甲车间产品较乙车间产品稳定.
,故甲车间产品较乙车间产品稳定.
例3 在某次有奖销售中,每10万份奖券中有一个头奖(奖金10000元) ,2个二等奖(奖金5000元),500个三等奖(奖金100元),10000个四等奖(奖金5元) .试求每张奖券平均获利多少?(假设所有奖券全部卖完,每张奖券面值3元.)
解:设每张奖券的奖金为T,则T的频率分布为
|
T |
10000 |
5000 |
100 |
5 |
0 |
|
P |
 |
 |
 |
 |
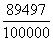 |
平均付利=
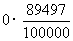
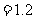 ,每张奖券获利3-1.2=1.8元.
,每张奖券获利3-1.2=1.8元.
例4 给出施化肥量对水稻产量影响的试验数据:
|
施化肥量x |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
水稻产量y |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
(1)画出上表的散点图;(2)求出回归直线.
解:(1)散点图(略).
(2)表中的数据进行具体计算,列成以下表格
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
xi |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
yi |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
|
xiyi |
4950 |
6900 |
9125 |
12150 |
15575 |
18000 |
20475 |
 , , |
故可得到 
从而得回归直线方程是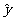 =4.75 x+257.
=4.75 x+257.
[追踪训练]
2. 已知样本99,100,101,x,y的平均数是100,方差是2,则xy=_____996________
1.已知 ,
, 之间的一组数据:
之间的一组数据:
 |
0 |
1 |
2 |
3 |
 |
1 |
3 |
5 |
7 |
则 与
与 的线性回归方程
的线性回归方程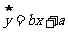 必过 (B )
必过 (B )
A.(2,2)点 B.(1.5,0)点 C.(1,2)点 D.(1.5,4)点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com