
1.导数概念的理解.
12. 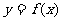

(1) 恒成立 ∴
恒成立 ∴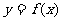 为
为 上
上
∴ 对任意 不等式
不等式  恒成立
恒成立
(2) 恒成立 ∴
恒成立 ∴ 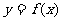 在
在 上
上
∴ 对任意 不等式
不等式 恒成立
恒成立
11. 导数与函数的单调性的关系
㈠ 与
与 为增函数的关系。
为增函数的关系。
 能推出
能推出 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数 在
在 上单调递增,但
上单调递增,但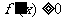 ,∴
,∴ 是
是 为增函数的充分不必要条件。
为增函数的充分不必要条件。
㈡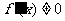 时,
时, 与
与 为增函数的关系。
为增函数的关系。
若将 的根作为分界点,因为规定
的根作为分界点,因为规定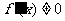 ,即抠去了分界点,此时
,即抠去了分界点,此时 为增函数,就一定有
为增函数,就一定有 。∴当
。∴当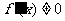 时,
时, 是
是 为增函数的充分必要条件。
为增函数的充分必要条件。
㈢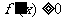 与
与 为增函数的关系。
为增函数的关系。
 为增函数,一定可以推出
为增函数,一定可以推出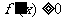 ,但反之不一定,因为
,但反之不一定,因为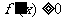 ,即为
,即为 或
或 。当函数在某个区间内恒有
。当函数在某个区间内恒有 ,则
,则 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴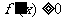 是
是 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,要谨慎处理。
㈣单调区间的求解过程,已知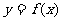
(1)分析 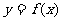 的定义域; (2)求导数
的定义域; (2)求导数 
(3)解不等式 ,解集在定义域内的部分为增区间
,解集在定义域内的部分为增区间
(4)解不等式 ,解集在定义域内的部分为减区间
,解集在定义域内的部分为减区间
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数 在某个区间内可导。
在某个区间内可导。
㈤函数单调区间的合并
函数单调区间的合并主要依据是函数 在
在 单调递增,在
单调递增,在 单调递增,又知函数在
单调递增,又知函数在 处连续,因此
处连续,因此 在
在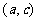 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
10.商的导数
两个函数的商的求导法则,课本中未加证明,只要求记住并能运用就可以。现补充证明如下:
设
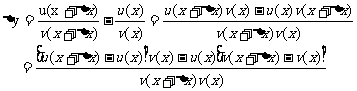

因为v(x)在点x处可导,所以它在点x处连续,于是△x→0时,v(x+△x)→v(x),从而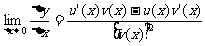 即
即 。
。
说明:(1)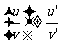 ; (2)
; (2)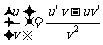
学习了函数的和、差、积、商的求导法则后,由常函数、幂函数及正、余弦函数经加、减、乘、除运算得到的简单的函数,均可利用求导法则与导数公式求导,而不需要回到导数的定义去求。
8.和(或差)的导数
上一节我们学习了常见函数的导数公式,那么对于函数 的导数,又如何求呢?我们不妨先利用导数的定义来求。
的导数,又如何求呢?我们不妨先利用导数的定义来求。


我们不难发现 ,即两函数和的导数等于这两函数的导数的和。
,即两函数和的导数等于这两函数的导数的和。
由此我们猜测在一般情况下结论成立。事实上教材中证明了我们的猜想,这就是两个函数的和(或差)的求导法则。
9.积的导数
两个函数的积的求导法则的证明是本节的一个难点,证明过程中变形的关键是依据导数定义的结构形式。(具体过程见课本P120)
说明:
(1)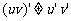 ;
;
(2)若c为常数,则(cu) ′=cu′。
7.导数的几何意义
函数y=f(x)在点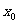 处的导数,就是曲线y=(x)在点
处的导数,就是曲线y=(x)在点 处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步:
处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步:
(1)求出函数y=f(x)在点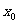 处的导数,即曲线y=f(x)在点
处的导数,即曲线y=f(x)在点 处的切线的斜率;
处的切线的斜率;
(2)在已知切点坐标和切线斜率的条件下,求得切线方程为

特别地,如果曲线y=f(x)在点 处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为
处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为
6.导数的定义
导数定义与求导数的方法是本节的重点,推导导数运算法则与某些导数公式时,都是以此为依据.
对导数的定义,我们应注意以下三点:
(1)△x是自变量x在
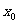 处的增量(或改变量).
处的增量(或改变量).
(2)导数定义中还包含了可导或可微的概念,如果△x→0时, 有极限,那么函数y=f(x)在点
有极限,那么函数y=f(x)在点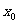 处可导或可微,才能得到f(x)在点
处可导或可微,才能得到f(x)在点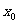 处的导数.
处的导数.
(3)如果函数y=f(x)在点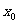 处可导,那么函数y=f(x)在点
处可导,那么函数y=f(x)在点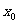 处连续(由连续函数定义可知).反之不一定成立.例如函数y=|x|在点x=0处连续,但不可导.
处连续(由连续函数定义可知).反之不一定成立.例如函数y=|x|在点x=0处连续,但不可导.
由导数定义求导数,是求导数的基本方法,必须严格按以下三个步骤进行:
(1)求函数的增量 ;
;
(2)求平均变化率 ;
;
(3)取极限,得导数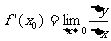 。
。
5.瞬时速度
在高一物理学习直线运动的速度时,涉及过瞬时速度的一些知识,物理教科书中首先指出:运动物体经过某一时刻(或某一位置)的速度叫做瞬时速度,然后从实际测量速度出发,结合汽车速度仪的使用,对瞬时速度作了说明.物理课上对瞬时速度只给出了直观的描述,有了极限工具后,本节教材中是用物体在一段时间运动的平均速度的极限来定义瞬时速度.
4.曲线的切线
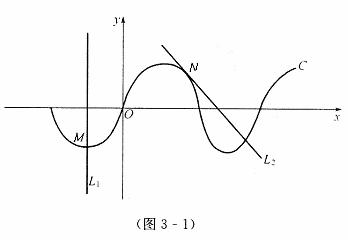
在初中学过圆的切线,直线和圆有惟一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,惟一的公共点叫做切点.圆是一种特殊的曲线,能不能将圆的切线的概念推广为一段曲线的切线,即直线和曲线有惟一公共点时,直线叫做曲线过该点的切线,显然这种推广是不妥当的.如图3-1中的曲线C是我们熟知的正弦曲线y=sinx.直线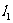 与曲线C有惟一公共点M,但我们不能说直线
与曲线C有惟一公共点M,但我们不能说直线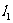 与曲线C相切;而直线
与曲线C相切;而直线 尽管与曲线C有不止一个公共点,我们还是说直线
尽管与曲线C有不止一个公共点,我们还是说直线 是曲线C在点N处的切线.因此,对于一般的曲线,须重新寻求曲线的切线的定义.所以课本利用割线的极限位置来定义了曲线的切线.
是曲线C在点N处的切线.因此,对于一般的曲线,须重新寻求曲线的切线的定义.所以课本利用割线的极限位置来定义了曲线的切线.
3.导数与解析几何或函数图象的混合问题是一种重要类型,也是高考中考察综合能力的一个方向,应引起注意。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com