
补充题:1.若 ,比较
,比较 与
与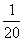 的大小
的大小
解:
 -
-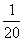 =……=
=……=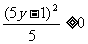 ∴
∴ ≥
≥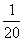
2.比较2sinq与sin2q的大小(0<q<2p)
略解:2sinq-sin2q=2sinq(1-cosq)
当qÎ(0,p)时2sinq(1-cosq)≥0 2sinq≥sin2q
当qÎ(p,2p)时2sinq(1-cosq)<0 2sinq<sin2q
3.性质1、2
2.性质2:如果 ,
, 那么
那么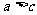 (传递性)
(传递性)
证:∵ ,
, ∴
∴ ,
,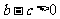
∵两个正数的和仍是正数 ∴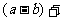

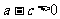 ∴
∴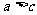
由对称性、性质2可以表示为如果 且
且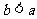 那么
那么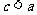
1.性质1:如果 ,那么
,那么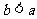 ;如果
;如果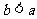 ,那么
,那么 (对称性)
(对称性)
证:∵ ∴
∴ 由正数的相反数是负数
由正数的相反数是负数
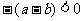

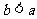
3.设 且
且 ,
,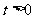 比较
比较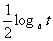 与
与 的大小
的大小
解: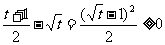 ∴
∴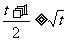
当 时
时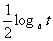 ≤
≤ ;当
;当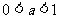 时
时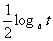 ≥
≥
2. 和
和
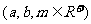
解:(取差) -
-
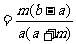 ∵
∵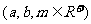
∴当 时
时 >
> ;当
;当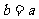 时
时 =
= ;当
;当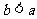 时
时 <
<
2.应用:例一 比较 与
与 的大小
的大小
解:(取差) -
-

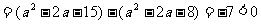
∴ <
<
例二 已知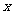 ¹0,
比较
¹0,
比较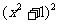 与
与 的大小
的大小
解:(取差)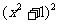 -
-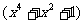

∵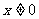 ∴
∴ 从而
从而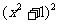 >
>
小结:步骤:作差-变形-判断-结论
例三 比较大小1. 和
和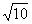
解:∵
∵
∴ <
<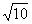
1.从实数与数轴上的点一一对应谈起
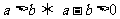
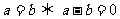
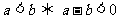
2.“绝对不等式与矛盾不等式”
1.“同向不等式与异向不等式”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com