
7. 已知sin(45° - a) =
已知sin(45° - a) = 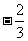 ,且45° < a < 90°,求sina .
,且45° < a < 90°,求sina .
8试求函数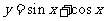
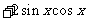
 的最大值和最小值。若
的最大值和最小值。若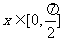 呢?
呢?
[师生互动]
6.已知α、β为锐角,cosα= ,tan(α-β)=-
,tan(α-β)=-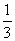 ,求Cosβ的值。
,求Cosβ的值。
5.已知tanα、tanβ是方程x2-3x-3=0的两个根,求sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β)的值。
|
学生质疑 |
|
|
教师释疑 |
|
4.设a,bÎ(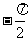 ,
,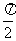 ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程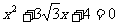 的两个根,求 a + b.
的两个根,求 a + b.
3.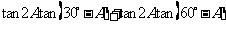
+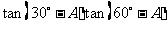
2.若0<α<β<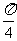 ,sinα+cosα=
,sinα+cosα=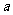 ,sinβ+cosβ=b,则( )
,sinβ+cosβ=b,则( )
A ab<1 B a>b
C a<b D ab>2
1. 在△ABC中,ÐC>90°,则tanAtanB与1的关系适合 ( )
A tanAtanB>1 B tanAtanB>1
C tanAtanB =1 D 不确定
4、证明
(1)证明基本方法:化繁为简法、左右归一法、变更命题法
注意:条件等式的证明关键在于分析已知条件与求证结论之间的差异与联系。
重点难点
重点:两角和与差的余弦、正弦、正切公式
难点:灵活应用和、差角公式进行化简、求值、证明
[自学评价]
两角和与差的正、余弦公式






[精典范例]
例1求值:(1)
(2)sin18°和cos36°
 例2已知
例2已知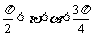 ,
,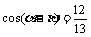 ,
,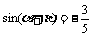 ,求sin2a的值。
,求sin2a的值。
例3已知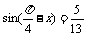 ,
,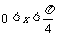 求
求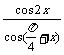 的值。
的值。
例4 若 且
且
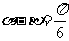 ,求
,求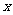 的值。
的值。
例5 已知锐角a, b, g 满足sina+sing=sinb, cosa-cosg=cosb, 求a-b的值。
例6已知tana,tanb是关于x的一元二次方程x2+px+2=0的两实根,求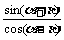 的值。
的值。
 例7 若
例7 若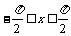 ,求f (x)=
,求f (x)=
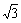 sinx
sinx
+cosx的最大值和最小值,并求出此时的x值。
例8 已知f (x)=-acos2x-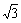 asin2x
asin2x
+2a+b,其中a>0,xÎ[0,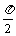 ]时,-5≤f (x)≤1,设g(t)=at2+bt-3,tÎ[-1,0],求g(t)的最小值。
]时,-5≤f (x)≤1,设g(t)=at2+bt-3,tÎ[-1,0],求g(t)的最小值。
思维点拔:
无论是化简、求值还是证明都要注意:角度的特点、函数名称的特点;其中切弦互化是常用手段;三角变换公式要灵活应用,注意角的范围对解题的影响,同时要掌握有关解题技巧:化弦、辅助角、角变换、公式逆用、正余弦和积互换。
[追踪训练]:
3、求值
(1)求值问题的基本类型:给角求值;给值求值;给值求角;给式求值
(2)技巧与方法:切化弦、异角化同角、异名化同名、角的变换
2、化简
(1)化简目标:项数尽量少
(2)化简基本方法:异角化同角;异名化同名;切割化弦;常值代换
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com