
2.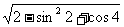 的值等于( )
的值等于( )
A。sin2 B。-cos2
C。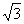 cos2
D。-
cos2
D。-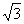 cos2
cos2
1. 若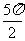 ≤α≤
≤α≤ ,则
,则
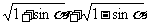 等于( )
等于( )

2、 这种形式的正切半角公式不需考虑符号,要简单。
这种形式的正切半角公式不需考虑符号,要简单。
[精典范例]
例1化简: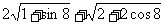
[解]
例2求证:[sinq(1+sinq)+cosq(1+cosq)]×[sinq(1-sinq)+cosq(1-cosq)] = sin2q
[证明]
[思维点拨]
关于“升幂”“降次”的应用:在二倍角公式中,“升次”“降次”与角的变化是相对的。在解题中应视题目的具体情况灵活掌握应用。
例3求函数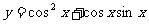 的值域。
的值域。
[解]
例4求证: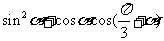
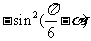 的值是与a无关的定值。
的值是与a无关的定值。
[证]
例5 化简:
 [解]
[解]
例6 求证:
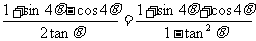
[证明]
 例7利用三角公式化简:
例7利用三角公式化简:

[解]
[追踪训练]
4、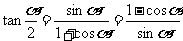 。
。
说明:1、用正切的半角公式显然行不同(带正负号),回到基本关系式,并向右边看齐;
3、这三个公式的开方形式称为半角公式,不要求记忆,但推导方法要掌握。
2、如果知道cosα的值和α角的终边所在象限,就可以将右边开方,从而求得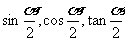 ;
;
1、在倍角公式中,以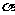 代替
代替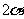 ,以
,以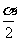 代替
代替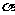 ,即得;
,即得;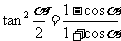 则将(1)(2)相除即得。
则将(1)(2)相除即得。
1.有关公式:
(1)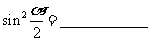 ;
;
(2)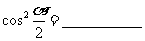 ;
;
(3)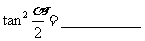 。
。
说明:
2.特别注意公式的三角表达形式,且要善于变形:
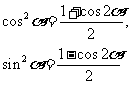
这两个形式今后常用。
学习要求
要求学生能较熟练地运用公式进行化简、求值、证明,增强灵活运用数学知识和逻辑推理能力
重点难点
重点:理解倍角公式,用单角的三角函数表示二倍角的三角函数
难点:灵活应用和、差、倍角公式进行三角式化简、求值、证明恒等式
[自学评价]
1.熟悉“倍角”与“二次”的关系(升角-降次,降角-升次)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com