
1.正弦定理的教学要达到“记熟公式”和“运算正确”这两个目标;
4.根据下列条件解三角形:
(1) ,
,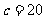 ,
, ;
;
(2) ,
,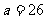 ,
, 。
。
[选修延伸]
[例3]在锐角三角形ABC中,A=2B, 、
、 、
、 所对的角分别为A、B、C,试求
所对的角分别为A、B、C,试求 的范围。
的范围。
分析:本题由条件锐角三角形得到B的范围,从而得出 的范围。
的范围。
[解]
 [例4]在△ABC中,设
[例4]在△ABC中,设
 ,求
,求 的值。
的值。
[解]
追踪训练二
(1)在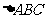 中,已知
中,已知 ,
, ,
, ,则
,则 ,
, .
.
(2)在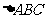 中,如果
中,如果 ,
, ,
, ,那么
,那么 ,
,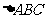 的面积是
.
的面积是
.
(3)在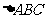 中,
中, ,
, ,则
,则 .
.

3.在△ABC中,
(1)已知 ,
, ,
, ,求
,求 ,
, ;
;
(2)已知 ,
, ,
, ,求
,求 ,
, .
.
2.在△ABC中,已知 ,
, ,
, ,则
,则 =
( )
=
( )
A
 B
B  C
C  D 1
D 1
1.在△ABC中, ,
, ,
, ,则
,则 的值为( )
的值为( )
A
 B
B 
C 10
D 
2.正弦定理可解决两类问题:
(1)________________________________;
(2)_________________________________
________________________________
[精典范例]
[例1]在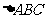 中,
中, ,
, ,
, ,求
,求 ,
, .
.
分析:正弦定理可以用于解决已知两角和一边求另两边和一角的问题.
[解]
[例2]根据下列条件解三角形:
(1) ;
;
(2) .
.
分析:正弦定理也可用于解决已知两边及一边的对角,求其他边和角的问题.
[解]
追踪训练一
1.正弦定理:在△ABC中, ______,
______,
2.正弦定理重点运用于三角形中“已知两角一边”、“已知两边一对角”等的相关问题
[课堂互动]
自学评价
1.正弦定理的证明方法有几种,但重点要突出向量证法;
1.1 正弦定理
第1课时
[学习导航]
知识网络
直角三角形的边角关系→任意三角形的边角关系→正弦定理
学习要求
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com