
4.两游艇自某地同时出发,一艇以10km/h的速度向正北行驶,另一艇以7km/h的速度向北偏东45°的方向行驶,问:经过40min,两艇相距多远?
略解:两艇相距4.71km
[选修延伸]
[例4]在△ABC中,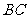 =
=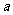 ,
,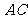 =
=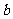 ,且
,且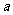 ,
,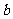 是方程
是方程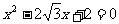 的两根,
的两根,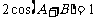 。
。
(1) 求角C的度数;
(2) 求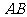 的长;
的长;
(3)求△ABC的面积。
解:(1) 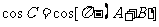
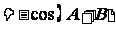

(2)因为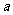 ,
,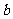 是方程
是方程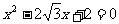 的两根,所以
的两根,所以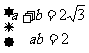


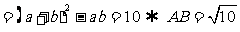
(3)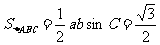
[例5]在△ABC中,角A、B、C所对的边分别为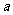 ,
,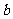 ,
,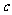 ,证明:
,证明:
 。
。
证明:由余弦定理知:
 ,
,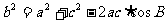
则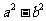
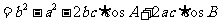 ,
,
整理得:
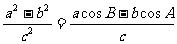 ,
,
又由正弦定理得:
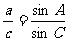 ,
, 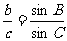 ,
,
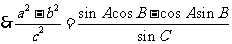
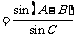
追踪训练二
3.在△ABC中,已知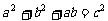 ,试求∠C的大小.
,试求∠C的大小.
略解: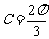
2.若三条线段的长为5,6,7,则用这三条线段( B ) A.能组成直角三角形
B.能组成锐角三角形
C.能组成钝角三角形
D.不能组成三角形
1.在△ABC中,
(1)已知A=60°,b=4,c=7,
求a;
(2)已知a=7,b=5,c=3,求A.
略解:(1)a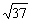
略解:(2)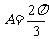
2.利用余弦定理,可以解决以下两类解斜三角形的问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.
[精典范例]
[例1]在 中,
中,
(1)已知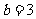 ,
,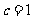 ,
,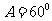 ,求
,求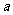 ;
;
(2)已知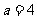 ,
,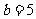 ,
,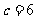 ,求
,求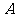 (精确到
(精确到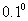 ).
).
[解](1)由余弦定理,得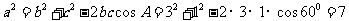 ,
,
所以 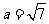 .
.
(2)由余弦定理,得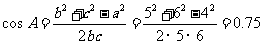 ,
,
所以,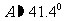 .
.
 点评: 利用余弦定理,可以解决以下两类解斜三角形的问题:(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.
点评: 利用余弦定理,可以解决以下两类解斜三角形的问题:(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.
[例2]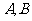 两地之间隔着一个水塘,现选择另一点
两地之间隔着一个水塘,现选择另一点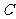 ,测得
,测得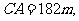

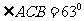 ,求
,求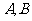 两地之间的距离(精确到
两地之间的距离(精确到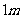 ).
).
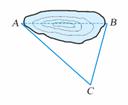 [解]由余弦定理,得
[解]由余弦定理,得
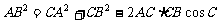
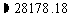
所以,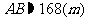
答 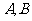 两地之间的距离约为
两地之间的距离约为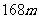 .
.
[例3]用余弦定理证明:在 中,当
中,当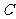 为锐角时,
为锐角时,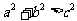 ;当
;当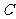 为钝角时,
为钝角时,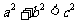 .
.
[证]当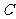 为锐角时,
为锐角时, ,由余弦定理,得
,由余弦定理,得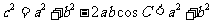 ,
,
即 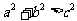 .
.
同理可证,当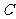 为钝角时,
为钝角时,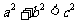
点评:余弦定理可以看做是勾股定理的推广.
追踪训练一
1.余弦定理:
(1)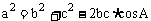 ,
,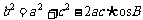 ,
,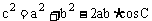 .
.
(2) 变形: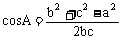 ,
,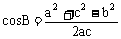 ,
,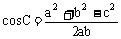
3. 能初步运用余弦定理解斜三角形.
[课堂互动]
自学评价
2. 体会向量的工具性;
1. 掌握余弦定理及其证明;
6.在△ABC中,
证明: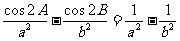 .
.
证明: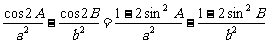
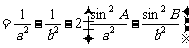
由正弦定理得: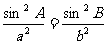
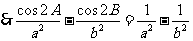
|

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com