
3.在等比数列{an}中,如果a6=6,a9=9,那么a3等于( )
A.4 B. C.
C. D.2
D.2
2.如图,在边长为1的等边三角形ABC中,连结各边中点得△A1B1C1,再连结△A1B1C1各边中点得△A2B2C2……如此继续下去,试证明数列S△ABC,
S△A1B1C1,S△A2B2C2,…是等比数列.

1. 三个数成等比数列,它们的积等于27,它们的平方和等于91,求这三个数.
三个数成等比数列,它们的积等于27,它们的平方和等于91,求这三个数.
3.对于k、l、m、n∈N*,若 ,则_________________;
,则_________________;
[选修延伸]
[例1](1)在等比数列{an}中,是否有a2n=an-1 an+1(n≥2)?
(2)如果数列{an}中,对于任意的正整数n(n≥2),都有a2n=an-1 an+1,那么,{an}一定是等比数列吗?
[解]
[例2]如图,一个边长为1的正三角形,将每边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)……试求第n个图形的边长和周长.



[解]
追踪训练一
2.等比数列的递增和递减性.
在等比数列{an}中
(1)若a1>0,q>1或a1<0,0<q<1则数列递增,
(2)若a1>0,0<q<1,或a1<0,q>1 ,则数列递减;
(3)若q=1,则数列为_____________;
(4)若q<0,则数列为____________.
1.如果an≠0,且an+12=anan+2对任意的n∈N*都成立,则数列{an}___________.
2. 掌握等比数列的通项公式,并能运用公式解决一些简单的实际问题.
[自学评价]
1.进一步体会等比数列是用来刻画一类离散现象的重要数学模型,理解等比数列的概念,
1.(2009南宁)南宁市狮山公园计划在健身区铺设广场砖.现有甲、乙两个工程队参加竞标,甲工程队铺设广场砖的造价 (元)与铺设面积
(元)与铺设面积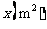 的函数关系如图12所示;乙工程队铺设广场砖的造价
的函数关系如图12所示;乙工程队铺设广场砖的造价 (元)与铺设面积
(元)与铺设面积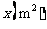 满足函数关系式:
满足函数关系式: .
.
(1)根据图12写出甲工程队铺设广场砖的造价 (元)与铺设面积
(元)与铺设面积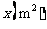 的函数关系式;
的函数关系式;
(2)如果狮山公园铺设广场砖的面积为 ,那么公园应选择哪个工程队施工更合算?
,那么公园应选择哪个工程队施工更合算?
解:(1)当 时,设
时,设 ,把
,把 代入上式得:
代入上式得:
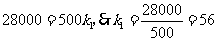
 ·················································································································· 2分
·················································································································· 2分
当 时,设
时,设 ,把
,把 、
、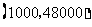 代入上式得:
代入上式得:
 ··································································································· 3分
··································································································· 3分
解得: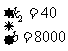 ·········································································································· 4分
·········································································································· 4分
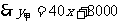
 ···················································································· 5分
···················································································· 5分
(2)当 时,
时, ················································· 6分
················································· 6分
 ·············································································· 7分
·············································································· 7分
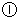 当
当 时,即:
时,即:
得: ··················································································································· 8分
··················································································································· 8分
 当
当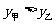 时,即:
时,即: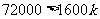
得: ············································································································· 9分
············································································································· 9分
 当
当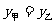 时,即
时,即 ,
,
答:当 时,选择甲工程队更合算,当
时,选择甲工程队更合算,当 时,选择乙工程队更合算,当
时,选择乙工程队更合算,当 时,选择两个工程队的花费一样.···························································································································· 10分
时,选择两个工程队的花费一样.···························································································································· 10分
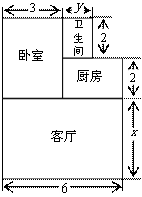 2(09钦州)小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:
2(09钦州)小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位: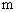 ),解答下列问题:
),解答下列问题:
(1)写出用含x、y的代数式表示的地面总面积;
(2)已知客厅面积比卫生间面积多21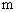 2,且地面总面积是卫生间面积的15倍,铺1
2,且地面总面积是卫生间面积的15倍,铺1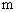 2地砖的平均费用为80元,求铺地砖的总费用为多少元?
2地砖的平均费用为80元,求铺地砖的总费用为多少元?
解:(1)地面总面积为:(6x+2y+18)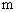 2;···························································· 4分
2;···························································· 4分
(2)由题意,得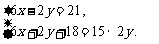 ······················································· 6分
······················································· 6分
解之,得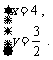 ····················································································· 8分
····················································································· 8分
∴地面总面积为:6x+2y+18=6×4+2× +18=45(
+18=45(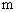 2).·············· 9分
2).·············· 9分
∵铺1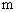 2地砖的平均费用为80元,
2地砖的平均费用为80元,
∴铺地砖的总费用为:45×80=3600(元).·········································· 10分
3(09湖南)为迎接“建国60周年”国庆,我市准备用灯饰美化红旗路,需采用A、B两种不同类型的灯笼200个,且B灯笼的个数是A灯笼的 。
。
(1)求A、B两种灯笼各需多少个?
(2)已知A、B两种灯笼的单价分别为40元、60元,则这次美化工程购置灯笼需多少费用?
(1)设需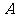 种灯笼
种灯笼 个,
个, 种灯笼
种灯笼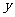 个,根据题意得:
个,根据题意得:
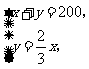 ··············································································································· 4分
··············································································································· 4分
解得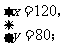 ·············································································································· 6分
·············································································································· 6分
(2)120×40+80×60=9600(元).············································································· 8分
4(09定西)图(1)是一扇半开着的办公室门的照片,门框镶嵌在墙体中间,门是向室内开的.图(2)画的是它的一个横断面.虚线表示门完全关好和开到最大限度(由于受到墙角的阻碍,再也开不动了)时的两种情形,这时二者的夹角为120°,从室内看门框露在外面部分的宽为4cm,求室内露出的墙的厚度a的值.(假设该门无论开到什么角度,门和门框之间基本都是无缝的.精确到0.1cm,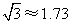 )
)

解从图中可以看出,在室内厚为acm的墙面、宽
为4cm的门框及开成120°的门之间构成了一
个直角三角形,且其中有一个角为60°.·········· 3分
从而 a=4×tan60° ·············································· 6分
=4× ≈6.9(cm).·································· 8分
≈6.9(cm).·································· 8分
即室内露出的墙的厚度约为6.9cm.
5(09河池)铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70﹪)售完,那么超市在这两次苹果销售中共盈利多少元?
解:(1)设试销时这种苹果的进货价是每千克 元,依题意,得······························· (1分)
元,依题意,得······························· (1分)
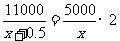 ··············································································· (5分)
··············································································· (5分)
解之,得 
 5···················································································· (6分)
5···················································································· (6分)
经检验,
 5是原方程的解.······························································· (7分)
5是原方程的解.······························································· (7分)
(2)试销时进苹果的数量为: (千克)
(千克)
第二次进苹果的数量为:2×1000 2000(千克)········································· (8分)
2000(千克)········································· (8分)
盈利为: 2600×7+400×7×0.7-5000-11000 4160(元) ······················ (9分)
4160(元) ······················ (9分)
答:试销时苹果的进货价是每千克5元,商场在两次苹果销售中共盈利4160元.
·············································· (10分)
 6(09南宁)如图,要设计一个等腰梯形的花坛,花坛上底长
6(09南宁)如图,要设计一个等腰梯形的花坛,花坛上底长 米,下底长
米,下底长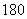 米,上下底相距
米,上下底相距 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为 米.
米.
(1)用含 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
.解:(1)横向甬道的面积为: ··········································· 2分
··········································· 2分
(2)依题意: ·············································· 4分
·············································· 4分
整理得: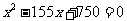
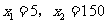 (不符合题意,舍去)······································································· 6分
(不符合题意,舍去)······································································· 6分
 甬道的宽为5米.
甬道的宽为5米.
(3)设建设花坛的总费用为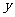 万元.
万元.
 ············································ 7分
············································ 7分

当 时,
时,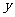 的值最小.··························································· 8分
的值最小.··························································· 8分
因为根据设计的要求,甬道的宽不能超过6米,
 米时,总费用最少.······················································································ 9分
米时,总费用最少.······················································································ 9分
最少费用为: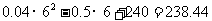 万元·················································· 10分
万元·················································· 10分
7(09本溪)为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买 支钢笔需要花
支钢笔需要花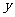 元,请你求出
元,请你求出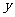 与
与 的函数关系式;
的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
解(1)解:设每个笔记本 元,每支钢笔
元,每支钢笔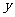 元.·························································· 1分
元.·························································· 1分
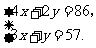 ············································································································· 2分
············································································································· 2分
 解得
解得
答:每个笔记本14元,每支钢笔15元.······································································· 5分
|

(3)当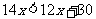 时,
时,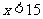 ;
;
当 时,
时, ;
;
当 时,
时, .···················································································· 8分
.···················································································· 8分
综上,当买超过10件但少于15件商品时,买笔记本省钱;
当买15件奖品时,买笔记本和钢笔一样;
当买奖品超过15件时,买钢笔省钱.·········································································· 10分
 8(09泉州)如图,等腰梯形花圃ABCD的底边AD靠墙,另三边用长为40米的铁栏杆围成,设该花圃的腰AB的长为x米.
8(09泉州)如图,等腰梯形花圃ABCD的底边AD靠墙,另三边用长为40米的铁栏杆围成,设该花圃的腰AB的长为x米.
(1)请求出底边BC的长(用含x的代数式表示);
(2)若∠BAD=60°, 该花圃的面积为S米2.
①求S与x之间的函数关系式(要指出自变量x的取值范围),并求当S= 时x的值;
时x的值;
②如果墙长为24米,试问S有最大值还是最小值?这个值是多少?
解:(1)∵AB=CD=x米,∴BC=40-AB-CD=(40-2x)
 ……………………………………………………(3分)
……………………………………………………(3分)
(2)①如图,过点B、C分别作BE⊥AD于E,CF⊥AD于F,在Rt△ABE中,AB=x,∠BAE=60°
∴AE=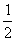 x,BE=
x,BE=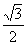 x.同理DF=
x.同理DF=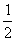 x,CF=
x,CF=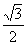 x
x
又EF=BC=40-2x
∴AD=AE+EF+DF=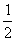 x+40-2x+
x+40-2x+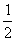 x=40-x……………………………(4分)
x=40-x……………………………(4分)
 ∴S=
∴S=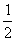 (40-2x+40-x)·
(40-2x+40-x)·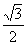 x=
x= x(80-3x)
x(80-3x)
= (0<x<20)…………………………………(6分)
(0<x<20)…………………………………(6分)
当S= 时,
时, =
=
解得:x1=6,x2=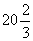 (舍去).∴x=6………………………………(8分)
(舍去).∴x=6………………………………(8分)
②由题意,得40-x≤24,解得x≥16,
结合①得16≤x<20………………………………………………………………(9分)
由①,S= =
=
∵a=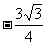 <0
<0
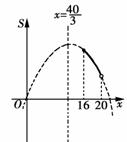
∴函数图象为开口向下的抛物线的一段(附函数图象草图如左).
其对称轴为x= ,∵16>
,∵16> ,由左图可知,
,由左图可知,
当16≤x<20时,S随x的增大而减小……………………………(11分)
∴当x=16时,S取得最大值,………………………………………(12分)
此时S最大值= .…………………(13分)
.…………………(13分)
9(09衢州)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:

|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价x(元/千克) |
400 |
|
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量y(千克) |
30 |
40 |
48 |
|
60 |
80 |
96 |
100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
解:(1) 函数解析式为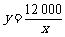 . ……2分
. ……2分
填表如下:
|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价x(元/千克) |
400 |
300 |
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量y(千克) |
30 |
40 |
48 |
50 |
60 |
80 |
96 |
100 |
……2分
(2) 2 104-(30+40+48+50+60+80+96+100)=1 600,
即8天试销后,余下的海产品还有1 600千克. ……1分
当x=150时, =80. ……2分
=80. ……2分
1 600÷80=20,所以余下的这些海产品预计再用20天可以全部售出. ……1分
10(09衢州)2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
 (1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
(1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
 (2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3) 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
解:(1) 18日新增甲型H1N1流感病例最多,增加了75人; ……4分
(2) 平均每天新增加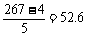 人, ……2分
人, ……2分
继续按这个平均数增加,到5月26日可达52.6×5+267=530人; ……2分
(3) 设每天传染中平均一个人传染了x个人,则
 ,
,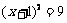 ,
,
解得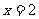 (x = -4舍去). ……2分
(x = -4舍去). ……2分
再经过5天的传染后,这个地区患甲型H1N1流感的人数为
(1+2)7=2 187(或1+2+6+18+54+162+486+1 458=2 187),
即一共将会有2 187人患甲型H1N1流感. ……2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com