
1.等差数列的通项公式:
①普通式: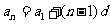 ;
;
②推广式:________________;
③变式: ;
;
 ;
;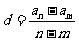 ;
;
注:等差数列通项公式的特征:等差数列的通项公式为关于项数n的次数不高于一次的多项式函数即an=An+B(若{an}为常数列时,A=0).
2、 掌握“叠加法”求等差数列通项公式的方法,掌握等差数列的通项公式,并能用公式解决一些简单的问题;
[自学评价]
1、 体会等差数列是用来刻画一类离散现象的重要数学模型,理解等差数列的概念;
6.已知数列{an}中a3=2,a7=1,又数列{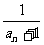 }为等差数列,则a11等于(
)
}为等差数列,则a11等于(
)
A.0 B.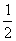 C.
C. D.-1
D.-1

5.在-1和8之间插入两个数a,b,使这四个数成等差数列,则a=______,b=______.
4.在等差数列{an}中,若a3=50,a5=30,则a7=______.
3.已知等差数列{an}的前3项依次为a-1,a+1,2a+3,则此数列的通项an为( )
A.2n-5 B.2n-3
C.2n-1 D.2n+1
2.等差数列{an}中,a2=-5,d=3,则a1为( )
A.-9 B.-8 C.-7 D.-4
1. 数列{an}的通项公式an=2n+5,则此数列( )
数列{an}的通项公式an=2n+5,则此数列( )
A.是公差为2的等差数列
B.是公差为5的等差数列
C.是首项为5的等差数列
D.是公差为n的等差数列
4.已知数列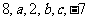 是等差数列,求未知项
是等差数列,求未知项 的值。
的值。
[解]
[选修延伸]
[例4]在等差数列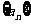 中,已知
中,已知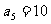 ,
, ,求
,求
分析: 先根据两个独立的条件解出两个量a1和d,进而再写出an的表达式.几个独立的条件就可以解出几个未知量,这是方程组的重要应用.
[解法一]:
思考:在此题中,有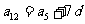 ,思考,能否不求首项
,思考,能否不求首项 ,而将
,而将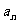 求出?
求出?
[解法二]:
思维点拔:
等差数列的通项公式涉及到四个量a1、an、n、d,用方程的观点知三求一。列方程组求基本量是解决等差数列问题的常用方法,注意通项公式更一般的形式:
[例5]若 ,则
,则 成等差数列。
成等差数列。
[证明]
思维点拔:
当已知a、b、c成等差数列时,通常采用2b=a+c作为解决问题的出发点.
[追踪训练二]:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com