
3. 顾客采用分期付款的方式购买一件5000元的商品,在购买一个月后第一次付款,且每月等额付款一次,在购买后的第12个月将货款全部付清,月利率0.5%.按复利计算,该顾客每月应付款多少元?
[答案]顾客每月应付款430元
2.我国1980年底人口以十亿计算.
(1)若我国人口年增长率为1.2%,则到2005年底我国约有多少人口?
(2)要使我国到2010年底人口不超过14亿,那么人口的年平均增长率最高是多少?
[答案]
(1)2005年底我国约有13.5亿人口
(2)人口的年平均增长率最高是1.1%
1. 回答我国古代用诗歌形式提出的一个数列问题:
远望巍巍塔七层,红灯向下成倍增,
共灯三百八十一,试问塔顶几盏灯?
[答案]塔顶3盏灯
3.375‰,按复利计算,每月等额还贷一次,并从贷款后的次月初开始还贷.如果10年还清,那么每月应还贷多少元?
分析:对于分期付款,银行有如下规定:
(1)分期付款为复利计息,每期付款数相同,且在期末付款;
(2)到最后一次付款时,各期所付的款额的本利之和等于商品售价的本利之和.
为解决上述问题,我们先考察一般情形.设某商品一次性付款的金额为a元,以分期付款的形式等额地分成n次付清,每期期末所付款是x元,则分期付款方式可表示为:

从而有
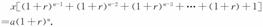
运用等比数列求和公式,化简得
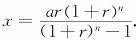
这就是分期付款的数学模型.
[解] 设每月应还贷x元,共付款
12×10=120次,则有

化简得

答 每月应还贷款2029.66元.
追踪训练一
3. 当 时,
时, ,这里
,这里 ,但
,但 ,这是等比数列前
,这是等比数列前 项和公式特征,据此判断数列
项和公式特征,据此判断数列 是否为等比数列
是否为等比数列
[精典范例]
[例1]水土流失是我国西部大开发中最突出的生态问题.全国9100万亩的坡耕地需要退耕还林,其中西部地区占70%.国家确定2000年西部地区退耕土地面积为515万亩,以后每年退耕土地面积递增12%,那么从2000年起到2005年底,西部地区退耕还林的面积共有多少万亩(精确到万亩)?
[解]根据题意,每年退耕还林的面积比上一年增长的百分比相同,所以从2000年起,每年退耕还林的面积(单位:万亩)组成一个等比数列 ,其中
,其中

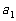 =515,q=1+12%=1.12,n=6,
=515,q=1+12%=1.12,n=6,
则
答 从2000年起到2005年底,西部地区退耕还林的面积共有4179万亩.
[例2]某人2004年初向银行申请个人住房公积金贷款20万元购买住房,月利率
2.若 是等比数列,且公比
是等比数列,且公比 ,则数列
,则数列 ,…是等比数列;
,…是等比数列;
当 ,且
,且 为偶数时,数列
为偶数时,数列
 ,…是常数数列0,它不是等比数列.
,…是常数数列0,它不是等比数列.
1.对于分期付款,银行有如下规定:
(1)分期付款为复利计息,每期付款数相同,且在期末付款;
(2)到最后一次付款时,各期所付的款额的本利之和等于商品售价的本利之和.
2.提高分析、解决问题能力,能用等比数列的知识解决某些实际问题。
[自学评价]
1.进一步熟练掌握等比数列的通项公式和前n项和公式;
4. 定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列
定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列 是等和数列,且
是等和数列,且 ,公和为5,求
,公和为5,求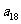 的值及这个数列的前
的值及这个数列的前 项和
项和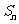 .
.
[解]  是等和数列,
是等和数列, ,公和为5,
,公和为5, ,则
,则 知
知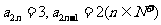 ,
,
 。数列
。数列 形如
形如 ,
, 。
。
答 3;当 为偶数时
为偶数时 ;当
;当 为奇数时,
为奇数时, .
.
|

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com