
例10已知数列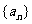 的前n项和
的前n项和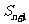 =4
=4 +2(n∈N+),a
+2(n∈N+),a =1.
=1.
(1)设 =
=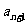 -2
-2 ,求证:数列
,求证:数列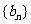 为等比数列,
为等比数列,
(2)设Cn= ,求证:
,求证: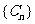 是等差数列.
是等差数列.
选题意图:本题考查等差、等比数列的定义及逻辑推理能力.
证明:(1) 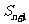 =4
=4 +2,
+2, 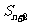 =4
=4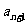 +2,相减得
+2,相减得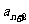 =4
=4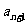 -4
-4 ,
,
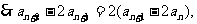
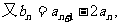


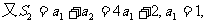
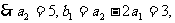
∴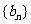 是以3为首项,2为公比的等比数列,∴
是以3为首项,2为公比的等比数列,∴ =3×2
=3×2 ?.
?.
(2) ∵


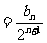


∴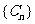 是以
是以 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
说明:一个表达式中既含有 又含有Sn,一般要利用
又含有Sn,一般要利用
 =
= -
- (n≥2),消去
(n≥2),消去 或
或 ,这里是消去了
,这里是消去了 .
.
例11在等比数列 中,
中, ,求
,求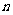 的范围.
的范围.
解:∵ ,∴
,∴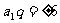
又∵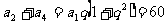 ,且
,且 ,∴
,∴ ,
,
∴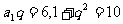 解之:
解之: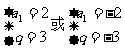
当 时,
时,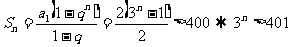 ,∴
,∴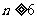
(∵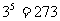
 )
)
当 时,
时, ,
,
∵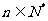 且必须为偶数
且必须为偶数
∴ ,(∵
,(∵ )
)
例12 设{ }, {
}, { }都是等差数列,它们的前n项和分别为
}都是等差数列,它们的前n项和分别为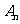 ,
,  , 已知
, 已知 ,求⑴
,求⑴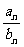 ;⑵
;⑵
 ⑴ 解法1:
⑴ 解法1: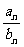 =
= =
=
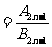 =
= .
.
⑴解法2:∵{ }, {
}, { }都是等差数列
}都是等差数列
∴可设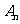 =kn(5n+3),
=kn(5n+3),  =kn(2n-1)
=kn(2n-1)
∴ =
=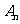 -
- = k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
 =
= -
- =k[n(2n-1)-(n-1)(2(n-1)-1)]
=kn(4n-3),
=k[n(2n-1)-(n-1)(2(n-1)-1)]
=kn(4n-3),
∴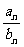 =
= =
=
⑵解:由⑴解法2,有
 =
=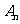 -
- = k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
 =
= -
- =k[n(2n-1)-(n-1)(2(n-1)-1)]
=kn(4n-3),
=k[n(2n-1)-(n-1)(2(n-1)-1)]
=kn(4n-3),
∴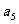 =k
=k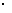 5
5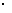 (10
(10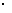 5-2)=240k
5-2)=240k
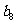 =k
=k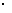 8
8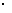 (4
(4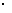 8-3)=232k
8-3)=232k
∴  =
=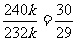
[追踪训练]
1.一等差数列共有9项,第1项等于1,各项之和等于369,一等比数列也有9项,并且它的第1项和最末一项与已知的等差数列的对应项相等,求等比数列的第7项。
解:设等差数列为{an},公差为d,等比数列为{bn},公比为q.
由已知得:a =b
=b =1,
=1,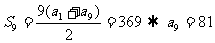 ?
?
又b =a
=a ,∴q
,∴q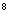 =81,∴q
=81,∴q =3,
=3,
∴b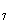 =b
=b q
q =27,即等比数列的第7项为27.
=27,即等比数列的第7项为27.
 说明:本题涉及的量较多,解答要理清关系,以免出错.?
说明:本题涉及的量较多,解答要理清关系,以免出错.?
(三)、数列求和的常用方法:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等。
1. 公式法:适用于等差、等比数列或可转化为等差、等比数列的数列。
2.裂项相消法:适用于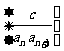 其中{
其中{  }是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等。
}是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等。
3.错位相减法:适用于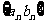 其中{
其中{  }是等差数列,
}是等差数列,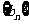 是各项不为0的等比数列。
是各项不为0的等比数列。
4.倒序相加法: 类似于等差数列前n项和公式的推导方法。
5.常用结论
1):
1+2+3+...+n = 
2) 1+3+5+...+(2n-1) =
3)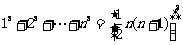
4) 
5) 

6) 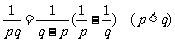
[精典范例]
一 函数方程思想在研究数列问题中的运用
 函数作为高中数学最重要的内容,几乎贯穿中学数学的始终,数列作为特殊的函数,与函数有着千丝万缕的联系:
函数作为高中数学最重要的内容,几乎贯穿中学数学的始终,数列作为特殊的函数,与函数有着千丝万缕的联系:
数列的通项公式及前n项和公式都是关于n的函数,当d≠0时,等差数列的通项是关于n的一次函数,前n项和是关于n的一元二次函数;等比数列的通项公式及前n项和公式都与指数函数有关。
在解决数学问题的过程中,把变量之间的制约关系用函数关系反映出来,便形成了函数思想;把众多待求量通过列方程、解方程来确定,便形成了方程思想,函数与方程之间的辩证思维便形成了函数方程思想。
因此,我们可以借助于函数的有关性质来研究数列问题。
例1(1)首项为正数的等差数列{a },其中S
},其中S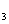 =S
=S ,问此数列前几项和最大?
,问此数列前几项和最大?
(2)等差数列{a }中,S
}中,S =100,S
=100,S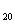 =300,求 S
=300,求 S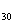 。
。
(3)等差数列的公差不为0,a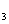 =15,a
=15,a ,a
,a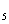 ,a
,a 成等比数列,求S
成等比数列,求S 。
。
分析 (1)等差数列前n项和S =
=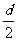 n
n +(a
+(a -
-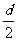 )n(d≠0)是关于n的二次函数且常数项为0,故可设S
)n(d≠0)是关于n的二次函数且常数项为0,故可设S =An
=An +B
+B ,运用配方法求最值;
,运用配方法求最值;
(2)由S =An
=An +B
+B 及S
及S =100,S
=100,S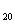 =300,求出A、B后再求S
=300,求出A、B后再求S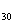 。
。
(3)求S 的关键,在于求a
的关键,在于求a ,由a
,由a =dn+(a
=dn+(a -d)(d≠0)知,它是关于n的一次函数,故可设a
-d)(d≠0)知,它是关于n的一次函数,故可设a = An+B,由条件列出方程组求A、B。
= An+B,由条件列出方程组求A、B。
[解](1)设S = An
= An +B
+B (A≠0),
(A≠0),
∵S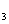 =S
=S ,
,
∴9A+3B=121A+11B,即14A+B=0。
又∵S = An
= An +B
+B =A(n+
=A(n+ )
) -
- ,
,
∴当n=- =7时,S
=7时,S 有最大值S
有最大值S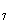 。
。
另解由S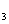 =S
=S ,得a
,得a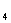 +a
+a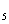 +a
+a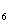 +a
+a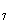 +a
+a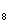 +a
+a +a
+a +a
+a =0,
=0,
又∵a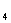 + a
+ a = a
= a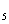 + a
+ a = a
= a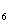 + a
+ a = a
= a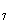 +a
+a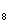 ,
,
∴4(a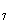 +a
+a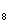 )=0, a
)=0, a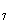 +a
+a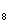 =0.
=0.
由于a >0,据题意知a
>0,据题意知a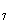 =-a
=-a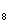 >0,a
>0,a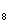 <0
<0
因此,前7项和最大。
 (2)设S
(2)设S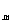 =An
=An +Bn(A≠0)
+Bn(A≠0)
∵S =100,S
=100,S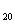 =300,
=300,
∴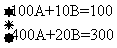

∴S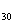 =900×
=900× +30×5=600。
+30×5=600。
另解 ∵S =100,S
=100,S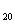 =300,又S
=300,又S ,S
,S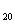 -S
-S ,S
,S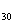 -S
-S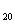 成等差数列。
成等差数列。
∴S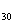 -S
-S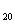 =2(S
=2(S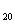 -S
-S )-S
)-S
∴S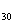 =600
=600
(3)设a =An+B(A≠0)
=An+B(A≠0)
∵a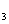 =15,a
=15,a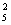 =a
=a ·a
·a ,
,
∴ 
∴ 
a =2n-1
=2n-1
∴S =(2×1-1)+(2×2-1)+…+(2×n-1)
=(2×1-1)+(2×2-1)+…+(2×n-1)
=2×(1+2+…+n)-n
=n(n+1)-n=n .
.
评析 从函数角度考察等差数列中的通项公式,前n项和公式,从而把数列问题转化为函数解决,体现了函数的思想和方法的应用。
二 求数列的通项公式
数列的通项公式是数列的核心之一,它如同函数中的解析式一样,有解析式便可研究其性质等;而有了数列的通项公式便可求出任一项及前n项和等,看来,求数列的通项往往是解题的突破口、关键点,现将求数列通项公式的几种题目类型及方法总结如下。
1. 观察法
观察法就是观察数列特征,横向看各项之间的关系结构,纵向看各项与项数n的内在联系,从而归纳出数列的通项公式。
例2写出下面各数列的一个通项公式
 (1)
(1) ,
,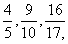 …;
…;
(2)1,- …;
…;
(3) …;
…;
(4)21,203,2005,20007,…;
(5)0.2,0.22,0.222,0.2222,…;
(6)1,0,1,0,…;
(7)1,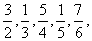 …
…
[解](1)注意各项的分子分别是1 ,2
,2 ,3
,3 ,4
,4 ,…,分母比分子大1,
,…,分母比分子大1,
∴数列的通项公式为a =
=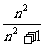 .
.
(2)奇数项为正,偶然项为负,各项分母可看作2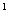 -1=1,2
-1=1,2 -1=3,2
-1=3,2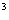 -1=7,2
-1=7,2 -1=15,2
-1=15,2 -1=31,…,各项分子均为1。
-1=31,…,各项分子均为1。
∴数列的通项公式为a =(-1)
=(-1) ·
·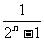
(3)各项的分母分别是2 ,2
,2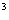 ,2
,2 ,2
,2 ,…分子比分母小1。
,…分子比分母小1。
∴数列的通项公式为a =
=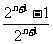
(4)各项可看作21=2×10+1203=2×100+32005=2×1000+5
20007=2×10000+7,
∴数列的通项公式为a =2×10
=2×10 +(2n-1).
+(2n-1).
(5)把各项适当变形0.2=2×0.1=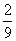 ×0.9=
×0.9=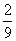 ×(1-
×(1- ),0.22=2×0.11=
),0.22=2×0.11=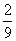 ×0.99=
×0.99=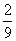 ×(1-
×(1- ),0.222=
),0.222=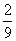 ×(1-
×(1-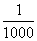 ),0.222=
),0.222=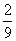 ×(1-
×(1-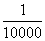 ),…,
),…,
∴数列的通项公式为a =
=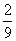 ·(1-
·(1-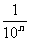 )。
)。
(6)奇数项皆为1,偶然项为0,
∴数列的通项公式为a =
=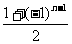
 (7)各项可看作1=1+0,
(7)各项可看作1=1+0, =
= +1,
+1,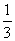 =
=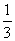 +0,
+0,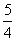 =
=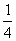 +1,
+1,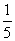 =
=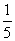 +0,
+0,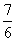 =
=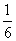 +1,…,∴数列的通项公式为a
+1,…,∴数列的通项公式为a =
=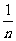 +
+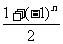 .
.
评析 用观察法写数列的通项公式,一般考虑如下几点:
(1)
观察数列各项符号变化,考虑通项公式中是否有(-1) 或者(-1)
或者(-1)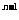 部分,如本例中(2),(6),(7)也有所涉及。
部分,如本例中(2),(6),(7)也有所涉及。
(2) 分解分子分母的因数(式),考虑其变化规律与序号的关系,应注意根据某些变化规律较明显的项,“猜”出某些因式约分后规律表现得不那么明显的项,同时要特别注意等差,等比关系,如本例(2),(3),(4)等。
(3)
考虑分子、分母与一些特殊数列如2 ,3
,3 ,n
,n ,n
,n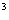 等的关系,如本例(1),(2),(3)等。
等的关系,如本例(1),(2),(3)等。
2. 已知S 求a
求a 或已知S
或已知S 与a
与a 的关系求a
的关系求a
已知数列{a }的前n项和S
}的前n项和S 求a
求a 时,要注意运用a
时,要注意运用a 和S
和S 的关系,即
的关系,即

例3已知下列各数列{a }的前n项和S
}的前n项和S 的公式,求{a
的公式,求{a }的通项公式。
}的通项公式。
(1)
S =10
=10 -1;(2)S
-1;(2)S =10
=10 +1;
+1;
[解](1)当n=1时,a =S
=S =9,
=9,
当n≥2时,a = S
= S -S
-S =(10
=(10 -1)-(10
-1)-(10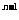 -1)=10
-1)=10 -10
-10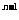 =9·10
=9·10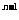 ,
,
且n=1时,a =9也适合上式,∴a
=9也适合上式,∴a =9·10
=9·10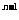 (n
(n ).
).
(2)当n=1时,a =S
=S =10
=10 +1=11,
+1=11,
当n≥2时,a = S
= S -S
-S =(10
=(10 +1)-(10
+1)-(10 +1)=9·10
+1)=9·10 ,
,
而n=1时,a =11,不适合上式,
=11,不适合上式,
∴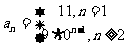
评析 已知{a }的前n项和S
}的前n项和S 求a
求a 时应注意以下三点:
时应注意以下三点:
(1)
应重视分类类讨论的应用,要先分n=1和n≥2两种情况讨论,特别注意由S -S
-S = a
= a 推导的通项a
推导的通项a 中的n≥2。
中的n≥2。
(2)
 由S
由S -S
-S = a
= a ,推得的a
,推得的a 且当n=1时,a
且当n=1时,a 也适合“a
也适合“a 式”,则需统一“合写”。
式”,则需统一“合写”。
(3)
由S -S
-S = a
= a 推得的a
推得的a ,当n=1时,a
,当n=1时,a 不适合“a
不适合“a 式”,则数列的通项应分段表示(“分号”),即
式”,则数列的通项应分段表示(“分号”),即 如本例中(2),(3)。请观察本例中(1)与(2)的差异及联系。
如本例中(2),(3)。请观察本例中(1)与(2)的差异及联系。
3. 累差法
若数列{a }满足a
}满足a -a
-a =f(n)(n
=f(n)(n ),其中{f(n)}是易求和数列,那么可用累差法求a
),其中{f(n)}是易求和数列,那么可用累差法求a 。(请你复习求等差数列通项公式的部分)
。(请你复习求等差数列通项公式的部分)
例4求数列1,3,7,13,21,…的一个通项公式。
[解] ∵a -a
-a =3-1=2,
=3-1=2,
a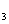 -a
-a =7-3=4,
=7-3=4,
a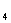 -a
-a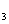 =13-7=6,
=13-7=6,
…
a -a
-a =2(n-1)
=2(n-1)
以上n-1个等式左右两边分别相加,得
a -a
-a =2[1+2+3+…+(n-1)]=(n-1)n,
=2[1+2+3+…+(n-1)]=(n-1)n,
∴a =n
=n -n+1.
-n+1.
且n=1时,a =1适合上式。
=1适合上式。
∴a =n
=n -n+1.
-n+1.
评析
我们应验证n=1时a =1适合a
=1适合a =n
=n -n+1式,这是什么原因。
-n+1式,这是什么原因。
4. 累商法
若数列{a }满足
}满足 =f(n)( n
=f(n)( n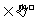 ),其中数列{f(n)}前n项积可求,则可用累商法求a
),其中数列{f(n)}前n项积可求,则可用累商法求a .
.
例5在数列{a }中,a
}中,a =2,a
=2,a =
=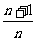 a
a ,求通项a
,求通项a 。
。
[解] ∵a =2,a
=2,a =
=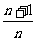 a
a ,
,
 ∴
∴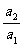 =
=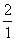 ,
,
 =
= ,
,
……
 =
=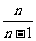 。
。
以上n-1个等式左右两边分别相乘得
 =n, a
=n, a =2n.
=2n.
且n=1时,a =2也适合上式。
=2也适合上式。
∴a =2n .
=2n .
5. 构造法
直接求通项a 较难求,可以通过整理变形等,从中构造出一个等差或等比数列,从而将问题转化为较易求解的问题,进一步求出通项a
较难求,可以通过整理变形等,从中构造出一个等差或等比数列,从而将问题转化为较易求解的问题,进一步求出通项a 。
。
例6各项非零的数列{a },首项a
},首项a =1,且2S
=1,且2S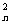 =2a
=2a S
S -a
-a ,n≥2,求数列的通项a
,n≥2,求数列的通项a 。
。
[解] ∵a =1,2S
=1,2S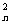 =2a
=2a S
S -a
-a , n≥2,又a
, n≥2,又a = S
= S -S
-S .
.
∴2S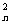 =2S
=2S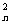 -2 S
-2 S S
S -S
-S + S
+ S ,
,
∴ -
-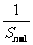 =2 (n≥2)(怎么得到的?)
=2 (n≥2)(怎么得到的?)
∴数列{ }是以
}是以 =1为首项,以2为公差的等差数列,
=1为首项,以2为公差的等差数列,
∴ =1+(n-1)·2=2n-1, S
=1+(n-1)·2=2n-1, S =
=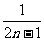 .
.
∴a = S
= S -S
-S =
=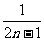 -
- =
=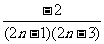 (n≥2)
(n≥2)
又a =S
=S =1,不适合上式,
=1,不适合上式,
 ∴
∴
有些求通项的题目可能要综合应用几种方法和技巧;当然了,有些题可能有多种解法。
评析 构造法解决问题希大家尽量掌握,这对于提高我们的数学素质大有帮助。
注意 求数列通项公式的问题是最为常见的试题,特别要注意已知S 求a
求a 的问题。
的问题。
三 数列求和
数列求和是数列部分的重要内容,求和问题也是很常见的试题,对于等差数列,等比数列的求和主要是运用公式;某些既不是等差数,也不是等比数列的求和问题,一般有以下四种常用求和技巧和方法。
1.公式法
能直接应用等差数列或等比数列的求和公式以及正整数平方和,立方和公式寻求和的方法。
例7数列{a }的通项a
}的通项a =n
=n -n,求前n项和S
-n,求前n项和S 。
。
[解] S =(1
=(1 -1)+(2
-1)+(2 -2)+…+(n
-2)+…+(n -n)
-n)
=(1 +2
+2 +…+n
+…+n )-(1+2+…+n)
)-(1+2+…+n)
=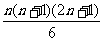 -
-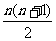
=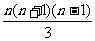 。
。
2.倒序求和法
3.错项求和法
[例2]求和S =
= +
+ +
+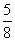 +…+
+…+ 。
。
请你独立完成,相信你会有更深的体会。
答案 S =3-
=3-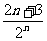 。
。
4.裂拆项法
例8在数列{a }中,a
}中,a =10
=10 +2n-1,求S
+2n-1,求S
[解] S =(10
=(10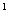 +2×1-1)+(10
+2×1-1)+(10 +2×2-1)+…(10
+2×2-1)+…(10 +2n-1)
+2n-1)
=(10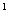 +10
+10 +…+10
+…+10 )+2×(1+2+…+n)-n
)+2×(1+2+…+n)-n
=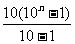 +n(n+1)-n
+n(n+1)-n
= (10
(10 -1)+n
-1)+n .
.
 注意 把通项进行合理地分拆与组合,转化为易求和的数列的求和问题。
注意 把通项进行合理地分拆与组合,转化为易求和的数列的求和问题。
练习:求数列1,1+2,1+2+3,…的前n项的和。
答案 S =
=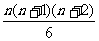 。
。
例9已知数列{a }:
}: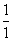 ,
,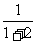 ,
, ,…
,…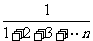 ,…,求它的前n项和。
,…,求它的前n项和。
分析 我们先看通项a =
=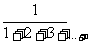 =
= ,然后想什么办法求S
,然后想什么办法求S 呢?将通项分裂成两项之差如何?
呢?将通项分裂成两项之差如何?
[解]∵a =
= =2(
=2( ), (为什么呢?)
), (为什么呢?)
∴S =a
=a +a
+a +a
+a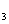 +…+a
+…+a
=2[(1- )+(
)+( -
-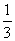 )+(
)+(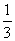 -
-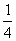 )+…+(
)+…+( )]
)]
=2(1- )=
)=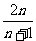 。 (成功了!)
。 (成功了!)
评析 如果数列的通项公式可转化为f(n+1)-f(n)形式,常采用裂项求和的方法,特别地,当数列的通项公式是关于n的分式形式时,可尝试采用此法。
常用的裂项技巧如: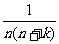 =
=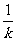 (
( );
);
 =
=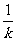 (
( -
-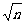 )等。
)等。
使用裂项法时要注意正负项相消时,消去了哪些项,保留了哪些项;你是否注意到由于数列{a }中每一项a
}中每一项a 均裂成一正一负两项,所以互为相反数的项合并为零后,所剩正数项与负数项的项数必是一样多的,切不可漏写未被消去的项。
均裂成一正一负两项,所以互为相反数的项合并为零后,所剩正数项与负数项的项数必是一样多的,切不可漏写未被消去的项。
(二)等差数列和等比数列
1. 等差数列和等比数列的概念、有关公式和性质
|
|
等差数列 |
等比数列 |
|
|
定义 |
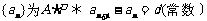 |
 |
|
|
通项公式 |
 = =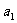 +(n-1)d= +(n-1)d=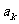 +(n-k)d= +(n-k)d= + +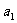 -d -d |
 |
|
|
求和公式 |
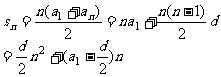 |
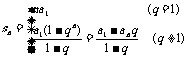 |
|
|
中项公式 |
A=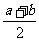 推广:2 推广:2 = =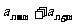 |
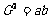 。 。推广:  |
|
|
性质 |
1 |
若m+n=p+q则 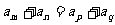 |
若m+n=p+q,则 。 。 |
|
2 |
若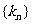 成A.P(其中 成A.P(其中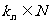 )则 )则 也为A.P。 也为A.P。 |
若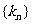 成等比数列 (其中 成等比数列 (其中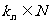 ),则 ),则 成等比数列。 成等比数列。 |
|
|
3 |
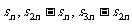 成等差数列。 成等差数列。 |
 成等比数列。 成等比数列。 |
|
|
4 |
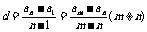 |
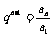 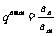  |
2. 判断和证明数列是等差(等比)数列常有三种方法:
判断和证明数列是等差(等比)数列常有三种方法:
(1)定义法:对于n≥2的任意自然数,验证 为同一常数。
为同一常数。
(2)通项公式法。
(3)中项公式法:验证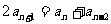
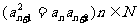 都成立。
都成立。
3. 在等差数列{ }中,有关Sn
的最值问题:
}中,有关Sn
的最值问题:
(1)当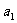 >0,d<0时,满足
>0,d<0时,满足 的项数m使得
的项数m使得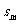 取最大值。
取最大值。
(2)当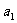 <0,d>0时,满足
<0,d>0时,满足 的项数m使得
的项数m使得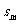 取最小值。
取最小值。
在解含绝对值的数列最值问题时,注意转化思想的应用。
(一)数列的概念
数列的定义(一般定义,数列与函数)、数列的表示法。
数列的通项公式。
求数列通项公式的一个重要方法:
对于任一数列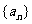 ,其通项
,其通项 和它的前n项和
和它的前n项和 之间的关系是
之间的关系是 
5.若等比数列{an}中,S4=2,S8=6,则a17+a18+a19+a20的值等于__32____.

|

4.等比数列{an}共2n项,其和为-240,且奇数项的和比偶数项的和大80,则公比q=___2___.
3.数列1,1+2,1+2+22,…,(1+2+22+…+2n-1),…,前n项和等于( B )
A.2n+1-n B.2n+1-n-2
C.2n-n D.2n
2.已知{an是公比为 的等比数列},若a1+a4+a7+…+a97=100,则a3+a6+a9+…+a99的值是(
A )
的等比数列},若a1+a4+a7+…+a97=100,则a3+a6+a9+…+a99的值是(
A )
A.25 B.50 C.75 D.125
1.已知等比数列{an}中,前n项和Sn=54,S2n=60,则S3n等于( C )
A.64 B.66
C.60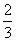 D.66
D.66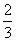
4.某企业年初有资金1000万元,如果该企业经过生产经营能使年资金平均增长率达到50%,但每年底都要扣除消费基金x万元,余下资金投入再生产,为实现经过5年资金达到2000万元(扣除消费基金后),那么每年应扣除消费基金多少万元(精确到万元)?
[解]设逐年扣除消费基金后的资金数组成一个数列 ,则
,则
a1=1000×(1+50%)-x=1000×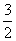 -x;
-x;
a2=(1000×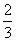 -x)(1+50%)-x
-x)(1+50%)-x
=1000×(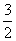 )2-(1+
)2-(1+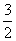 )x;
)x;
依次类推得a5=1000×(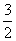 )5-[1+
)5-[1+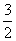 +(
+(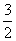 )2+(
)2+(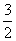 )3+(
)3+(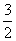 )4]x.
)4]x.
由题意知:
1000×(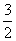 )5-[1+
)5-[1+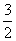 +(
+(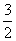 )2+(
)2+(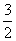 )3+(
)3+(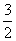 )4]x
)4]x
 =2000
=2000
解得x≈424万元
[选修延伸]
[例3]设数列 的首项a1=1,前n项的和Sn满足关系式3tSn-(2t+3)Sn-1=3t(t为常数,且t>0, n=2,3,4,……)。
的首项a1=1,前n项的和Sn满足关系式3tSn-(2t+3)Sn-1=3t(t为常数,且t>0, n=2,3,4,……)。
(1)求证:数列 是等比数列;
是等比数列;
(2)设 的公比为f(t),作数列
的公比为f(t),作数列 ,使得b1=1,bn=f(
,使得b1=1,bn=f(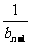 ) (n=2,3,4,…),求
) (n=2,3,4,…),求 的通项公式。
的通项公式。
(3)求和:b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1
[解](1)求得a1=S1=1 S2=a1+a2=1+a2,代入关系式,得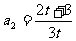 ,又3tSn-(2t+3)Sn-1=3t, 3tSn-1-(2t+3)Sn-2=3t, 两式相减得3tan-(2t+3)an-1=0,
,又3tSn-(2t+3)Sn-1=3t, 3tSn-1-(2t+3)Sn-2=3t, 两式相减得3tan-(2t+3)an-1=0,
∴
(2)由f(t)=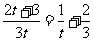
得bn=f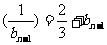
由此可得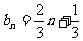
(3)原式
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=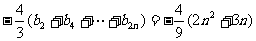
[例4]在数列 中,
中, 求数列
求数列 的前n项和Sn.
的前n项和Sn.
分析:要分成偶数项和奇数项之和分别求解。
[解]当n=2k(k∈N+)时,a1,a3,a5,…,a2k-1,…,成等差数列,公有效差为4,首项为1;而a2,a4,…,a2k,…成等比数列,公比为q,首项为a2=9,
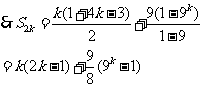 .
.
将k= 代入得
代入得
当n=2k-1时,由S2k-1=S2k-a2k,得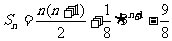 .
.
追踪训练二
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com