
1.数列的定义:按一定次序排列的一列数叫做叫做数列(sequence of number).
[注意]⑴数列的数是按一定次序排列的,因此,如果组成两个数列的数相同而排列次序不同,那么它们就是不同的数列;
⑵定义中并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现.
思考:简述数列与数集的区别.
数列强调数列中的项是有顺序的,数列中的项可以是相等的,与数集中的无序性和互异性是不同的.
4.提高观察、抽象的能力.
[自学评价]
3.理解数列的通项公式的概念,并会用通项公式写出数列的前几项,会根据简单数列的前几项写出它的一个通项公式;
2.理解数列和函数之间的关系,会用列表法和图象法表示数列;
1.理解数列概念,了解数列的分类;
6.已知函数f (x)=(x-1) , 数列{
, 数列{ }是公差为d的等差数列,数列{
}是公差为d的等差数列,数列{ }是公比为q的等比数列(q∈R, q≠1, q≠0),
}是公比为q的等比数列(q∈R, q≠1, q≠0),
若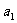 =f (d-1),
=f (d-1),  =f (d+1),
=f (d+1),  =f (q-1),
=f (q-1),  =f (q+1),
=f (q+1),
(1) 求数列{ }, {
}, { }的通项公式;
}的通项公式;
(2) 设数列{ }对任意的自然数n均有
}对任意的自然数n均有
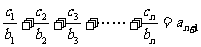 成立,求
成立,求 +
+ +
+ +……+
+……+ 的值.
的值.
解:(1) 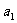 =f (d-1)=(d-2)
=f (d-1)=(d-2) ,
,  =f (d+1)=d
=f (d+1)=d ,
,
∴  -
-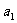 =2d,
即d
=2d,
即d -(d-2)
-(d-2) =2d,
=2d,
解得d=2, ∴ 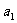 =0,
=0,  =2(n-1),
=2(n-1),
又 =f (q-1)=(q-2)
=f (q-1)=(q-2) ,
,  =f (q+1)=q
=f (q+1)=q ,
,  =q
=q ,
,
∴  =q
=q ,
,
∵q ≠1, ∴ q=3, ∴ =1,
=1,  =3
=3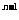
(2) 设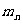 =
= (n∈N), 数列{
(n∈N), 数列{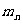 }的前n项和为
}的前n项和为 ,
,
则 =
=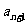 =2n,
=2n,
 =
= =2(n-1),
=2(n-1),
∴ -
- =2, 即
=2, 即 =2, ∴
=2, ∴  =2
=2 =2·3
=2·3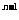
∴ +
+ +
+ +……+
+……+
=2+2·3 +……+2·3
+……+2·3 =
= =
=
5. 等差数列
等差数列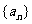 中,
中, ,
, ,依次抽出这个数列的第
,依次抽出这个数列的第 项,组成数列
项,组成数列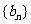 ,求数列
,求数列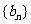 的通项公式和前
的通项公式和前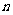 项和公式.
项和公式.
4.已知数列 ,
, ,
,
(1)求通项公式 ;
;
(2)若 ,求数列
,求数列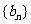 的最小项的值;
的最小项的值;
(3)数列 的前
的前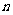 项和为
项和为 ,求数列
,求数列 前项的和
前项的和 .
.
3.已知等差数列{ }的前n项和为
}的前n项和为 ,
, =
= , 且
, 且
 =
= ,
, +
+ =21, (1) 求数列{bn}的通项公式;(2) 求证:
=21, (1) 求数列{bn}的通项公式;(2) 求证: +
+ +
+ +……+
+……+ <2.
<2.
解:(1)设等差数列{ }的首项为
}的首项为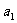 , 公差为d,则
, 公差为d,则
 =(
=(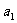 +2d)·
+2d)· =
= ,
,
 +
+ =8
=8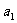 +13d=21, 解得
+13d=21, 解得 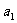 =1, d=1,
=1, d=1,
∴  =n,
=n,  =
=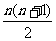 ,
,  =
= ;
;
(2)  +
+ +
+ +……+
+……+
=2·[(1- )+(
)+( -
-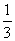 )+……+(
)+……+( )]<2.
)]<2.
2.已知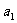 , a
, a ,
,  , …,
, …,  , …构成一等差数列,其前n项和为
, …构成一等差数列,其前n项和为 =n
=n , 设
, 设 =
= , 记{
, 记{ }的前n项和为
}的前n项和为 , (1) 求数列{
, (1) 求数列{ }的通项公式;(2) 证明:
}的通项公式;(2) 证明: <1.
<1.
解:(1) 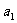 =
=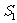 =1, 当n≥2时,
=1, 当n≥2时,  =
= -
- =2n-1;
=2n-1;
由于n=1时符合公式,∴  =2n-1 (n≥1).
=2n-1 (n≥1).
(2)  =
=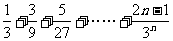 ,
,
∴ 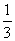
 =
= ,
,
两式相减得

 =
=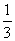 +
+ =
=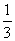 +
+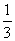 (1-
(1- )-
)- ,
,
∴  =
= +
+ (1-
(1- )-
)- <1.
<1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com