
2.数列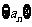 ,
,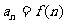 是一个函数,则它的定义域为
( )
是一个函数,则它的定义域为
( )
A. 非负整数集 B. 正整数集
C. 正整数集或其子集
D. 正整数集或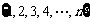
1.已知数列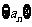 ,
,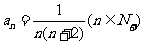 ,那么
,那么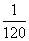 是这个数列的第 ( B )项.
是这个数列的第 ( B )项.
A. 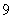 B.
B. 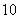 C.
C. 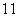 D.
D. 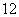
3.数列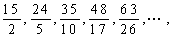 的一个通项公式为
的一个通项公式为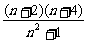 .
.
[选修延伸]
[例3]在数列{an}中,a1=2,a17=66,通项公式是项数n的一次函数.
(1)求数列{an}的通项公式;
(2)88是否是数列{an}中的项.
[解] (1)设an=An+B,由a1=2,a17=66
得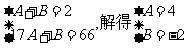
∴an=4n-2
(2)令an=88,即4n-2=88得n=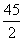
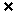 N*
N*
∴88不是数列{an}中的项.
思维点拔:已知数列的通项,怎样判断一个含有参数的代数式是否为数列中的项?
例如:已知数列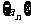 的通项为
的通项为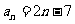 ,判断
,判断 是否为数列中的项?
是否为数列中的项?
提示:可把 化成通项公式的形式,即
化成通项公式的形式,即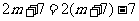 ,因为
,因为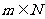 ,所以
,所以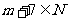 满足通项公式的意义,所以
满足通项公式的意义,所以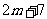 是数列中的第
是数列中的第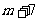 项.
项.
[追踪训练二]
2. 数列
数列 的一个通项公式是
( B )
的一个通项公式是
( B )
A. 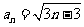 B.
B. 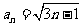
C. 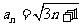 D.
D. 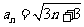
1.下列解析式中不是数列1,-1,1,-1,1,-1…,的通项公式的是 ( A )
A. 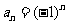 B.
B. 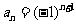
C. 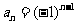 D.
D. 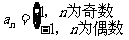
6.数列的表示形式:列举法,通项公式法和图象法
[精典范例]
[例1] 已知数列的第n项an 为2n-1,写出这个数列的首项、第2项和第3项.
[解]
首项为a1=2×1-1=1;
第2项为a2=2×2-1=3;
第3项为a3=2×3-1=5?
[例2]根据下面数列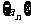 的通项公式,写出它的前5项,并作出它的图象:
的通项公式,写出它的前5项,并作出它的图象:
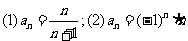
[解](1)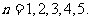
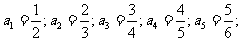
(2)
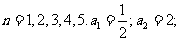
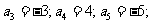
[例3]写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)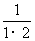 ,-
,-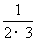 ,
, 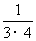 ,-
,-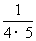 .
.
(2)0, 2, 0, 2
分析:写出数列的通项公式,就是寻找 与项数
与项数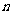 的对应关系
的对应关系
[解](1) 这个数列的前4项的绝对值都等于序号与序号加1的积的倒数,且奇数项为正,偶数项为负,所以它的一个通项公式是:
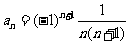
(2) 这个数列的奇数项为0,偶数项为2,所以它的一个通项公式是: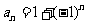
点评:(1)将数列的整数部分和分数部分进行分别处理,然后再整体合并;
(2) 将数列进行整体变形以便能呈现出与序号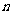 相关且便于表达的关系.
相关且便于表达的关系.
[追踪训练一]
5. 数列的图像都是一群孤立的点.
从映射、函数的观点来看,数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,数列的通项公式就是相应函数的解析式,因此,数列也可根据其通项公式画出其对应图象.
4.数列的通项公式:如果数列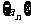 的第
的第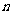 项与
之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式(the formula of general term).
项与
之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式(the formula of general term).
注意:⑴并不是所有数列都能写出其通项公式,如数列1,1.4,1.41, 1.414,…;
⑵一个数列的通项公式有时是不唯一的,如数列:1,0,1,0,1,0,…它的通项公式可以是
 ,
,
也可以是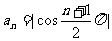 .
.
⑶数列通项公式的作用:
①求数列中任意一项;
②检验某数是否是该数列中的一项
3.数列的分类:
按项分类:有穷数列(项数有限);无穷数列(项数无限);
2.数列的项:数列中的每一个数都叫做这个数列的项(term). 各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,….
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com