
4.如果a,A,b成等差数列,那么A叫做a与b的等差中项;且
 。
。
[精典范例]
[例1]根据等差数列的概念,判断下列数列是否是等差数列;
(1)1,1,1,1,1,1
(2)4,7,10,13,16
(3)-3,-2,-1,0,1,2,3
[解]
(1)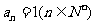
(2)
(3)
思考:如果一个数列 的通项公式为
的通项公式为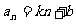 ,其中
,其中 都是常数,那么这个数列一定是等差数列吗?
都是常数,那么这个数列一定是等差数列吗?
是
[例2]求出下列等差数列中的未知项:
(1)3,a,5;
(2)3,b,c,-9.
[解](1)根据题意,得
a-3=5-a,
解得a=4.
(2)根据题意,得
b-3=c-b,
c-b=-9-c,
解得b=-1,c=-5
[例3]
 (1)求等差数列8,5,2…的第20项?
(1)求等差数列8,5,2…的第20项?
(2) 401是不是等差数列
401是不是等差数列 5,
5, 9,
9, 13,…的项?如果是,是第几项?
13,…的项?如果是,是第几项?
[解](1)
(2)是,第100项
[追踪训练一]:
2.等差数列的通项公式 ;
;
1.等差数列:一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列
(arithmetic progression),这个常数就叫做
等差数列的公差(common difference),常用字母“d”表示。
⑴公差d一定是由后项减前项所得,而不能用前项减后项来求;
⑵对于数列{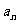 },若
},若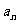 -
-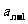 =d (与n无关的数或字母),n≥2,n∈N
=d (与n无关的数或字母),n≥2,n∈N ,则此数列是等差数列,d 为公差
,则此数列是等差数列,d 为公差
2、 掌握“叠加法”求等差数列通项公式的方法,掌握等差数列的通项公式,并能用公式解决一些简单的问题;
[自学评价]
1、 体会等差数列是用来刻画一类离散现象的重要数学模型,理解等差数列的概念;
4. 已知数列{an}的递推公式为
已知数列{an}的递推公式为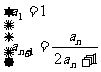 n∈N*,那么数列{an}的通项公式为______.
n∈N*,那么数列{an}的通项公式为______.
[解析]由a1=1,且an+1= 知a2=
知a2=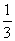 ,a3=
,a3=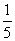 ,a4=
,a4= ∴an=
∴an=
[答案]an=
|
3.若数列{an}满足a1=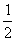 ,an=1-
,an=1- ,n≥2,n∈N*,则a2003等于( B
)
,n≥2,n∈N*,则a2003等于( B
)
A.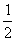 B.-1 C.2 D.1
B.-1 C.2 D.1
2.数列{-2n2+29n+3}中最大项的值是( B )
A.107 B.108 C.108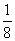 D.109
D.109
1.已知数列{an}的首项,a1=1,且an=2an-1+1(n≥2),则a5为( D )
A.7 B.15 C.30 D.31
4.设凸n边形的对角线条数为f(n),则f(3)=______;f(n+1)=______(用f(n)表示).
[解析]显然f(3)=0f(n+1)=f(n)+(n-1)
[答案]0 f(n)+n-1
[选修延伸]
[例4]已知数列 的通项为
的通项为
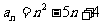 ,问:
,问:
(1).数列中有多少项为负数?
(2). 为何值时,
为何值时, 有最小值?并求此最小值.
有最小值?并求此最小值.
分析:数列的通项公式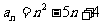 可看成
可看成 ,利用二次函数的性质解决问题.
,利用二次函数的性质解决问题.
[解](1)n=2或3共2项
(1)n=2或3时有最小值-2
点评:数列的项与项数之间构成特殊的函数关系,用函数的有关知识解决问题时,要考虑定义域为正整数这一约束条件.
[追踪训练二]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com