
1.(1998年全国高考)关于函数f(x)=4sin(2x+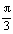 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f( )=f(
)=f(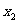 )=0可得x1-x2必是π的整数倍;
)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可以改写成y=4cos(2x- );
);
③y=f(x)的图像关于点(- ,0)对称;
,0)对称;
④y=f(x)的图像关于直线x=- 对称.
对称.
其中正确的命题序号是_________.(注:把你认为正确的命题序号都填上)
3. (1991年三南高考)已知函数f(x)=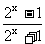 ⑴证明:f(x)在(-∞,+∞)上是增函数;
⑵证明:对不小于3的自然数n都有f(n)>
⑴证明:f(x)在(-∞,+∞)上是增函数;
⑵证明:对不小于3的自然数n都有f(n)>
.
[答案与提示:1. 当k在集合(-∞,-1)∪(0,1)内取值时,原方程有解;2.
a的取值范围为 ,(2)可用数学归纳法证明;3. 略.]
,(2)可用数学归纳法证明;3. 略.]
2.
(1990年全国高考)设f(x)=lg ,其中a是实数,n是任意给定的自然数,且n≥2.
①如果f(x)当x∈(-∞,1]时有意义,求a的取值范围;
②如果a∈(0,1),证明2f(x)<f(2x)当x≠0时成立.
,其中a是实数,n是任意给定的自然数,且n≥2.
①如果f(x)当x∈(-∞,1]时有意义,求a的取值范围;
②如果a∈(0,1),证明2f(x)<f(2x)当x≠0时成立.
当 时,
时,
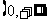 ,因此,若令
,因此,若令 ,则
,则
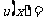

由
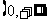 ,则
,则
 可知:此时
可知:此时 的取值范围为
的取值范围为 .
.
又 时,
时,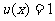 .所以,函数
.所以,函数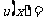
 的值域为
的值域为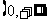 .
.
所以,函数 的值域为R.
的值域为R.
(2)设 ,则
,则 =
= ,利用
,利用 与
与 互为倒数,可得
互为倒数,可得 =
= ,所以,
,所以,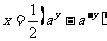 .
.
所以, =
= ,
, R.
R.
(3)任取 R,则
R,则 =
= =
= ,所以,函数
,所以,函数 为奇函数.
为奇函数.
任取
 ,且
,且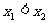 ,则由
,则由 及指数函数的性质可知:
及指数函数的性质可知:
 ,
,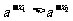 ,
,
所以, ,即
,即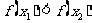 .
.
所以, 在定义域内单调递增.
在定义域内单调递增.
(4)由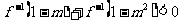 得:
得: ,即:
,即:
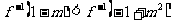
结合 的单调性可知:上式等价于:
的单调性可知:上式等价于: ,解之得:
,解之得: .
.
点评 ①定义域是研究函数的基础.求值域、判断奇偶性、单调性、研究函数图象等都应先从定义域出发.②从定义域出发,利用函数的单调性,是求函数值域常用的方法.
例2.已知函数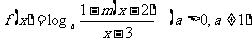 ,对定义域内的任意
,对定义域内的任意 都有
都有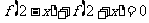 成立.
成立.
(1)求实数 的值;
的值;
(2)若当 时,
时, 的取值范围恰为
的取值范围恰为 ,求实数
,求实数 的值.
的值.
讲解:(1)由 及
及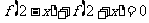 可得:
可得:

解之得: .
.
当 时,函数
时,函数 无意义,所以,只有
无意义,所以,只有 .
.
(2) 时,
时, ,其定义域为
,其定义域为
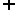
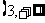 .
.
所以,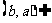
 或
或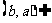
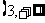 .
.
①若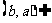
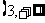 ,则
,则 .
.
为研究 时
时 的值域,可考虑
的值域,可考虑 在
在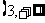 上的单调性.下证
上的单调性.下证 在
在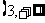 上单调递减.
上单调递减.
任取
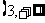 ,且
,且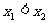 ,则
,则

又 ,所以,
,所以,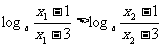 ,即
,即 .
.
所以,当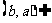
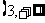 ,
, 在
在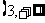 上单调递减
上单调递减
由题: 时,
时, 的取值范围恰为
的取值范围恰为 ,所以,必有
,所以,必有 ,解之得:
,解之得: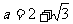 (因为
(因为 ,所以舍去
,所以舍去 )
)
②若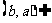
 ,则
,则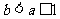 .又由于
.又由于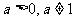 ,所以,
,所以, .
.
此时,同上可证 在
在 上单调递增(证明过程略).
上单调递增(证明过程略).
所以, 在
在 上的取值范围应为
上的取值范围应为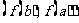 ,而
,而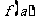 为常数,故
为常数,故 的取值范围不可能恰为
的取值范围不可能恰为 .
.
所以,在这种情况下, 无解.
无解.
综上,符合题意的实数 的值为
的值为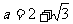 ,
,
点评 本题(2)中,充分的运用已知条件,可以减少分类讨论的次数.
高考真题
1. (1989年全国高考)已知a>0且a≠1,试求使方程
loga(x-ak)=loga2(x2-a2)有解的k的取值范围.
2.
(1989年全国高考)设 是定义在R上以2为周期的函数,对k∈Z,用
是定义在R上以2为周期的函数,对k∈Z,用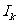 表示区间(2k-1,2
k+1),已知当
表示区间(2k-1,2
k+1),已知当 时,
时, .
①求
.
①求 在
在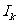 上的解析表达式;
②对自然数k,求集合
上的解析表达式;
②对自然数k,求集合 ={a|使方程
={a|使方程 =ax在
=ax在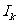 上有两个不相等的实根}
上有两个不相等的实根}
[答案与提示:1.增函数,证明略。2. ①当 时,
时,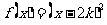 ;②对自然数k,集合
;②对自然数k,集合 =
=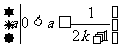 ]
]
1.
(2002年北京春季高考)已知 是偶函数,而且在
是偶函数,而且在 上是减函数,判断
上是减函数,判断 在
在 上是增函数还是减函数,并加以证明。
上是增函数还是减函数,并加以证明。
3. (1993年全国高考)已知关于x的实系数二次方程x 2 + ax +b =0有两个实数根a ,b. 证明:
(I ) 如果| a | < 2, | b | < 2, 那么2| a | < 4 + b且 | b | < 4 ;
(II) 如果2| a | < 4 + b 且 | b | < 4 , 那么| a | < 2 , | b | < 2 .
[答案与提示:1.不存在. 2.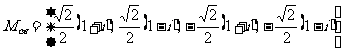 ,在其中任取两数,其和为零的概率为
,在其中任取两数,其和为零的概率为 ;证明略. 3.略. ]
;证明略. 3.略. ]
2.
(2001年上海高考)对任意一个非零复数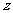 ,定义集合
,定义集合
(1)设 是方程
是方程 的一个根,用列举法表示集合
的一个根,用列举法表示集合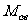 . 若在
. 若在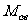 中任取两个数,求其和为零的概率.
中任取两个数,求其和为零的概率.
(2)设复数 ,求证:
,求证:
1. (1985年全国高考)设a,b是两个实数,A={(x,y)│x=n,y=na+b,n是整数},B={(x,y)│x=,m,y=3m2+15,m是整数},C={(x,y)│x2+y2≤144}是平面XOY内的点集合.讨论是否存在a和b使得
(1)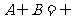 (
(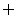 表示空集);(2)(a,b)∈C同时成立.
表示空集);(2)(a,b)∈C同时成立.
12.(09湖州)南极科考队使用酒精温度计而不是水银温度计,是由于酒精的
A.沸点低 B.密度小 C.凝固点低 D.比热大
答案:C
 (09成都). 去年春节前后,我国南方部分地区遭遇了低温雨雪天气,某些地区的树枝上甚至出现了图3所示的“雾凇”。“雾凇”和霜的形成过程很相似,都是
(09成都). 去年春节前后,我国南方部分地区遭遇了低温雨雪天气,某些地区的树枝上甚至出现了图3所示的“雾凇”。“雾凇”和霜的形成过程很相似,都是
A.水蒸气液化形成的 B.水蒸气凝华形成的
C.小水珠凝固形成的 D.小冰晶升华形成的
答案:B
(09河南)物理,留心观察皆学问。对以下现象解释正确的是
A.初冬季节,在家里洗澡时发现房间里充满“白气”,这些“白气”是水蒸气
B.在夏季的早晨看到足球场里的草叶上挂满了露珠,而到了初冬,露水不见了,却看到了薄薄的一层霜,有人认为霜是由露变成的
C.放在衣橱里的樟脑丸,时间久了会明显变小,是因为樟脑丸蒸发为气体跑掉了
D.把冰箱里的冻豆腐取出,冰化后,发现豆腐里有许多小孔,这是豆腐里的水先遇冷结冰,后又熔化成水形成的
答案:D
 (09山东潍坊).热现象在一年四季中随处可见,下列有关说法中正确的是
(09山东潍坊).热现象在一年四季中随处可见,下列有关说法中正确的是
A.春天的早晨经常出现大雾,这是汽化现象
B.夏天揭开冰棒包装后会看到冰棒冒“白汽”,这是凝华现象
C.秋天的早晨花草上出现小的露珠,这是液化现象
D.初冬的早晨地面上会出现白色的霜,这是凝固现象
答案:C
(09山东临沂).清晨草叶上常挂有晶莹的露珠,这是由于夜间温度低,空气中的水蒸气________形成的,在阳光照射下这些露珠又会慢慢消失,是由于露珠发生了_______的缘故。
答案:液化 汽化(蒸发)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com