2．不等关系的含义：

[答]　　　　　　　　　　　　　　　　

[精典范例]

例1：某博物馆的门票每位10元, 20人以上(含20人)的团体标8折优惠, 那么不足20人时, 应该选择怎样的购票策略?

[解]

点评:列式的前提是：设自变量，找不等关系.

例2：某杂志以每本2元的价格发行时, 发行量为10万册, 经过调查, 若价格每提高0.2元, 发行量就减少5000册, 要使杂志社的销售收入大于22.4万元, 每本杂志的价格应定在怎样的范围内.

[解]

点评：若设每本杂志价格为x元，则有

x[10-(x-2)]>22.4，化简略．

例3.下表给出了X、Y、Z三种食物的维生素的含量及成本:

某人欲将这三种食物混合成100kg的食品, 要使混合食品中至少含35000单位的维生素A及40000单位的维生素B , 设X , Y这两种食物各取x kg , ykg , 那么x , y应满足怎样的关系?

点评：列出的是二元一次不等式组，事实上，这里的x，y与100–x - y还都应该大于等于0．

思维点拔：

1．不等号有哪些？

[答] 　　　　　　　　　

4．提高观察、抽象的能力．

[课堂互动]

自学评价

3．总结建立不等式模型的基本思路．

2．经历由实际问题建立数学模型的过程, 体会其基本方法.

1．通过具体情境, 感受在观察现实世界时和日常生活中存在着的大量不等关系, 了解不等式(组)的实际背景．

重点：一元二次不等式的解法；二元一次不等式组表示的平面区域及线性规划问题；利用基本不等式进行不等式证明与求函数的最值．

难点：含参不等式的解法，线性规划中最优整数解的求法，不等式证明．

3.1 不等关系　

[学习导航]

知识网络

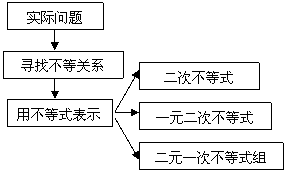
学习要求

3．利用基本不等式求最值或证明不等式，运用时往往需作适当的变形，创造条件应用基本不等式，常用变换技巧是“拆添项”“配凑因子”和“平方”等。应用基本不等式求最值时，要注意考虑三要素，即“一正二定三相等”。

[选修延伸]

柯西不等式

内容：

≥．

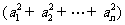
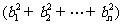
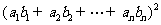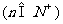
证明：设

．

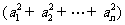
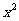
当＝0，即

时，柯西不等式显然成立．

当≠0，即

＞0时，

由于

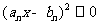恒成立．

于是,　化简变形即得

≥．

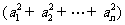
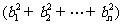
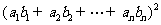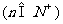
追踪训练

已知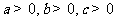，且，求证：

2．二元一次不等式(组)表示平面区域与线性规划问题是数形结合思想的运用。画平面区域是线性规划的基础，常用选点法定侧，注意边界是否在区域内。解线性规划应用题时要注意规范解题，写全解题步骤。

1．二次函数、一元二次方程和一元二次不等式是一个有机的整体，要深刻理解它们之间的相互关系，会用函数思想来研究方程和不等式．