1．进一步理解三个一元二次之间的关系，掌握一元二次不等式解的逆向问题。　

4．设k∈R , x₁ , x₂是方程x²－2kx+1－k²=0的两个实数根, 则x+x的最小值为

(　)

　 A. -2　 　 B. 0 　 C. 1　　　 D. 2

[选修延伸]

高次不等式的解法

解下列不等式：

(1)

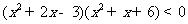
(2)

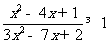
思维点拨

解高次不等式的方法步骤：

方法：序轴标根法．

步骤：①化一边为零且让最高次数系数为正；

②把根标在数轴上；

③右上方向起画曲线，让曲线依次穿过标在数轴上的各个根；

④根据“大于0在上方，小于0在下方”写出解集。

注：①重根问题处理方法：“奇过偶不过”．

②分式不等式转化为高次不等式求解．

追踪训练一

设(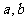为实常数)，且方程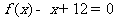有两个实数根为，，

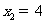(1)　　　 求函数的解析式．

(2)　　　 (2)设，解关于的不等式．

3. 函数y=lg(-x²+5x+24)的值小于1，则x的取值范围为________　　　 _____

2. 函数y=lg(2x²+3x-1)的定义域为_____________

1. 函数y=的定义域为____________

5．　　　 学会用化归的思想解决一些可化为一元二次不等式的问题。

追踪训练一

4．　　　 不等式的解要写成解集的形式，即用集合或区间表示。

3．　　　 解一元二次不等式的步骤：一看x²系数，二求方程的根，三写出结论。

2．　　　 解一元二次不等式的方法：图象法，结论法。

1．　　　 当a>0时ax²+bx+c>0的解集为两根之外或R，ax²+bx+c<0解集为两根之内或φ。