
1.理解算术平均数与几何平均数的定义及它们的关系.
3.已知函数
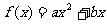 ,若
,若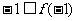
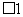 ,
,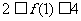 ,求
,求 的取值范围.
的取值范围.

1. 某工厂生产甲、乙两种产品,已知生产甲种产品1t,需矿石4t,煤3t,生产乙种产品1t,需矿石5t,煤10t,每1t甲种产品的利润是7万元,每1t乙种产品的利润是12万元,工厂在生产这两种产品的计划中,要求消耗矿石不超过200t,煤不超过300t,则甲、乙两种产品应各生产多少,能使利润总额达到最大?
|

|
A规格 |
B规格 |
C规格 |
||
|
第一种钢板 |
2 |
1 |
1 |
||
|
第二种钢板 |
1 |
2 |
3 |
今需A、B、C三种规格的成品分别为15 , 18 , 27块, 问各截这两种钢板多少张可得所需三种规格成品, 且使所用钢板张数最少?
|

2.整点最优解的求法:
(1)网格线法
(2)先求非整点最优解,然后定出目标函数的取值范围,再改变目标函数取值,定出整点最优解.
追踪训练
1.线性规划应用题的解题步骤:
(1)分析后将题中数据整理成一个表格;
(2)设自变量(通常为x,y,z等);
(3)列式(约束条件和目标函数);
(4)作可行域;
(5)作直线l0 :ax+by=0平移l0使其过最 优解的点;
(6)解相关方程组得最优解(根据需要可求出最值);
(7)作答.
2. 培养应用线性规划的知识解决实际问题的能力.
[课堂互动]
[精典范例]
例1.投资生产A产品时, 每生产100t需要资金200万元, 需场地200m2, 可获利润300万元; 投资生产B产品时, 每生产100米需资金300万元, 需场地100m2, 可获利润200万元, 现某单位可使用资金1400万元, 场地900m2, 问: 应作怎样的组合投资, 可使获利最大?
[解]
例2. 某运输公司向某地区运送物资, 每天至少运送180t , 该公司有8辆载重为6t的A型卡车与4辆载重为10t的B型卡车, 有10名驾驶员每辆卡车每天往返次数为A型车4次, B型车3次, 每辆卡车每天往返的成本费A型车为320元, B型车为504元, 试为该公司设计调配车辆方案, 使公司花费的成本最低.
思维点拔:
1. 能够将实际问题抽象概括为线性规划问题,明确解题步骤与整点最优解的求法
3.给出平面区域如图所示, 若使目标函数Z=ax+y (a>0), 取得最大值的最优解有无数个, 则a值为 ( )
A.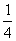 B.
B. 
C.
4
D. 


例2.设变量x , y满足条件 , 求S=5x+4y的最大值.
, 求S=5x+4y的最大值.
|
思维点拔:
求整点最优解的方法:
(1)作网格线法(特殊点可验证处理)求出的整数点逐一代入目标函数,求出目标函数的最值.
(2)作网格线,确定整点,然后设作l0让其平移确定最优整点解,再求最值.
追踪训练二
设变量x , y满足条件 , 求S=3x+2y的最值.
, 求S=3x+2y的最值.
2.已知 , 则4a-2b取值范围是__________
, 则4a-2b取值范围是__________
1. 已知 , 则目标函数Z=x+2y的最大值是___________ .
, 则目标函数Z=x+2y的最大值是___________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com