
1.画平面区域的步骤:
(1) 先画不等式对应的方程所表示的直线(包括直线时,把直线画成实线,不包括直线时,把直线画成虚线)简称"画线".
(2) 再通过选点法判定在直线的哪一侧.选点法中所选点常常为(0,0),(1,0)或(0,1)等,简称"定侧"
3.不等式x+y-1>0表示的平面区域:是直线x+y-1=0右上方的平面区域.
[精典范例]
例1.画出下列不等式所表示的平面区域
(1)y>-2x+1
(2)x-y+2>0
(3)y≤-2x+3
[解]
略.
例2. 已知P(x0 , y0)与点A(1 , 2)在直线l : 3x+2y-8=0两侧, 则 ( C )
A. 3x0+2y0>0
B. 3x0+2y0<0
C. 3x0+2y0>8
D. 3x0+2y0<8
思维点拔:
2.二元一次不等式表示平面区域的含义:
二元一次不等式解对应点构成的图形.
1.二元一次方程表示的图形 一条直线
3. 进一步体会数形结合的思想方法,开拓数学视野.
[课堂互动]
自学评价
2. 由二元一次不等式表示的平面区域能写出对应的不等式
1. 了解二元一次不等式的几何意义,会作出二元一次不等式表示的平面区域.
3.某渔业分司年初用98万元购买一艘捕鱼船, 第一年各种费用12万元, 以后每年都增加4万元, 每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后, 有两种处理方案: ①年平均获利最大时, 以26万元出售该渔船; ②总纯收入获利最大时, 以8万元出售该渔船, 问哪种方案最合算?
(提供公式: a>0
, x>0时, x+ ≥2
≥2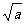 (当且仅当x=
(当且仅当x= 时取等号)
时取等号)
略解:(1)设第n年开始获利,则可得到: ,解后知第3年开始获利.
,解后知第3年开始获利.
(2)方案一:7年净获利110元.
方案二:10年净获利110元.
故方案一最合算.
[选修延伸]
分段函数模型
 某企业生产一种机器的固定成本为0.5万元, 但每生产100台时又需可变成本0.25万元, 市场对此商品的年需求量为500台, 销售收入函数为R(x)=5x-
某企业生产一种机器的固定成本为0.5万元, 但每生产100台时又需可变成本0.25万元, 市场对此商品的年需求量为500台, 销售收入函数为R(x)=5x- x2 (万元) (0≤x≤5). 其中x是产品售出的数量(单位: 百台)
x2 (万元) (0≤x≤5). 其中x是产品售出的数量(单位: 百台)
(1)把利润表示为年产量的函数;
(2)年产量为多少时, 企业所得的利润最大?
(3)年产量为多少时, 企业才不亏本?
略解:(1)设利润为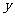 ,则
,则

(2)当且仅当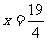 时,
时,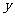 的最大值为
的最大值为 万元.
万元.
(3)由 ,解得
,解得
 即
即
答:略.
思维点拔:
|

2.某工厂的三年产值的年增长率情况依次为:第一年至少为a%,第二年至少为b%,第三年至少为c%,则这三年的年平均增长率至少为  .
.
1.制作一个高为20cm的长方体容器,其底面矩形的长比宽多10cm,并且容器的容积不得少于4000 ,则底面矩形的宽至少应为 10 ㎝.
,则底面矩形的宽至少应为 10 ㎝.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com