
2.整点: 坐标都是整数的点 .
[精典范例]
例1.画出下列不等式组所表示的区域
(1) 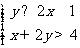
(2) 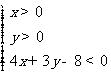
[解]
图略(见书).
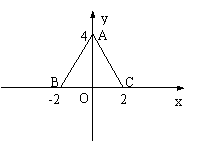 例2.如图, △ABC三个顶点A(0 , 4)
, B(-2 , 0) , C(2 , 0) , 求△ABC内任一点(x , y)所满足的条件.
例2.如图, △ABC三个顶点A(0 , 4)
, B(-2 , 0) , C(2 , 0) , 求△ABC内任一点(x , y)所满足的条件.
见书.
思维点拔:
1.不等式组表示的平面区域 各不等式表示平面区域的公共部分. .
2.学会解决一些简单的整点问题.
[课堂互动]
自学评价
1.理解二元一次不等式组表示平面区域的含义,并能准确地作出二元一次不等式组表示的平面区域,还能处理一些逆向问题.
5.已知两个点A(-3,-1)和B(4,-6)分布在直线-3x+2y+a=0的两侧,则a的取值范围为 (-7,24) .
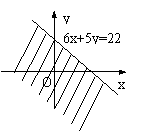
例2.将下列各图中的平面区域(阴影部分)用不等式表示出来. (图(1)中不包括y轴)
 |
|||
|
|||



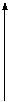 (1)
(2)
(1)
(2)
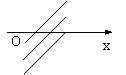
 (3)
(3)
|
 解:(1)
解:(1)
(2)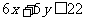
(3)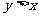
思维点拔:
有关画平面区域的逆向问题.需要注意如下两方面问题: (1)注意边界是虚线还是实线以确定不等式是否有"=".(2)选点法或用结论定侧,以确定不等式中的符号方向.
追踪训练
将下列各图中的平面区域(阴影部分)用不等式表示出来. (图(1)中不包括y轴)

(1)









|

|
(3)
解:(1)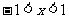
(2)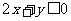
(3)
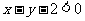
4.画出下列不等式表示的平面区域
(1)y≤x-1 (2)y<0
(3)3x-2y+6>0 (4)x>2
图略.
3.用"上方"或"下方"填空
若B<0,不等式Ax+By+C>0表示的区域在直线Ax+By+C=0的 下方 ;
不等式Ax+By+C<0表示的区域在直线Ax+By+C=0的 上方 .
2.不等式x+4y-9≥0表示直线 x+4y-9=0 ( C)
A.上方的平面区域
B. 下方的平面区域
C. 上方的平面区域(包括直线)
D. 下方的平面区域(包括直线)
1.判断下列命题是否正确
(1)点(0,0)在平面区域x+y≥0内 (是)
(2)点(0,0)在平面区域x+y+1<0内 (否)
(3)点(1,0)在平面区域y>2x内 (否)
(4)点(0,1)在平面区域x-y+1>0内 (否)
2.规律揭示
(1)直线y=kx+b把平面分成两个区域:y>kx+b表示直线上方的平面区域;
y<kx+b表示直线下方的平面区域.
(2)对于Ax+By+C>0(或<0)表示的区域:
当B>0时,Ax+By+C>0表示直线Ax+By+C=0上方的平面区域;
当B>0时,Ax+By+C<0表示直线Ax+By+C=0下方的平面区域.
追踪训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com