14. 甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，

答错得零分。假设甲队中每人答对的概率均为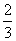，乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用ε表示甲队的总得分.

　　　 (Ⅰ)求随机变量ε分布列和数学期望；　　

(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).

13. 数学试题中共有10道选择题每道选择题都有4个选项，其中有且仅有一个是正确的.

评分标准规定：“每题只选1项，答对得5分，不答或答错得0分”，某考生每道题都给出了一个答案，已确定有6道题的答案是正确的，而其余题中，有两道题都可判断出两个选项是错误的，有一道题可以判断一个选项是错误的，还有一道题因不理解题意只能乱猜，试求出该考生：

(1)得50分的概率；

(2)得多少分的可能性最大.

12. 四个纪念币、、、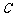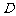,投掷时正面向上的概率如下表所示.

纪念币
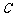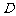概率

　　 这四个纪念币同时投掷一次,设表示出现正面向上的个数.

　 (1)求的分布列及数学期望；

　 (2)在概率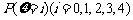中,若的值最大,求的取值范围.

11. 如图，面积为的正方形中有一个不规则的图形，可按下面方法估计的面积：在正方形中随机投掷个点，若个点中有个点落入中，则的面积的估计值为，假设正方形的边长为2，的面积为1，并向正方形中随机投掷个点，以表示落入中的点的数目．

(I)求的均值；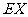

(II)求用以上方法估计的面积时，的面积的估计值与实际值之差在区间内的概率．

附表：

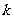
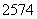
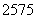
10. 甲、乙两人各射击一次，击中目标的概率分别是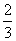和.假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响.

(Ⅰ)求甲射击4次,至少1次未击中目标的概率;

(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;

(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?

9. 一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率均为0.5，电话C、D占线的概率均为0.4。各部门是否占线相互之间没有影响。假设有部电话占线，试求随机变量的概率分布和它的期望。

8. 在一个盒子中，放有标号分别为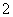，，的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为、，记．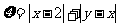

(Ⅰ)求随机变量的最大值，并求事件“取得最大值”的概率；

(Ⅱ)求随机变量的分布列和数学期望．

7. 甲、乙两支足球队，苦战120分钟，比分为1 ：1，现决定各派5名队员，每人射一个点球决定胜负，假设两支球队派出的队员点球命中率均为

⑴两队球员一个间隔一个出场射球，有多少种不同的出场顺序？

⑵甲、乙两队各射完5个点球后，再次出现平局的概率是多少？

6. 某同学上楼梯的习惯每步走1阶或2阶，现有一个11阶的楼梯 ，该同学从第1阶到第11阶用7步走完。

(1)求该同学恰好有连着三步都走2阶的概率；

(2)记该同学连走2阶的最多步数为ζ，求随机事件ζ的分布列及其期望。

5. 某售货员负责在甲、乙、丙三个柜面上售货．如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8，0.7．假定各个柜面是否需要照顾相互之间没有影响，求在这个小时内：

(1)只有丙柜面需要售货员照顾的概率；

(2)三个柜面最多有一个需要售货员照顾的概率；

(3)三个柜面至少有一个需要售货员照顾的概率．