

5.设a>0,b>0,则以下不等式不恒成立的是( )
A 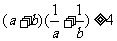 B
B 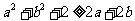
C 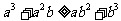 D
D 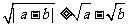
4.已知二次函数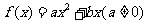 满足
满足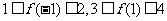 ,则
,则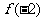 的 取值范围是__________________
的 取值范围是__________________
3.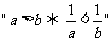 成立的充分必要条件是__________________
成立的充分必要条件是__________________
2.下列命题中,为真命题的是( )
A 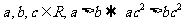 B
B 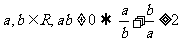
C 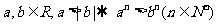 D
D 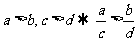
1.若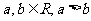 ,则( )
,则( )
A 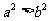 B
B 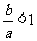 C
C 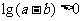 D
D 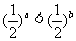
5.证明不等式常用方法:
(1)比较法(比差、商法); (2)综合法,分析法; (3)放缩法;
(4) 数学归纳法,函数单调性法,换元法,增量法,反证法等.
数学归纳法,函数单调性法,换元法,增量法,反证法等.
1.不等式的基本性质:
①若ab>0,则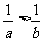 。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。
。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。
②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论。
③图象法:利用有关函数的图象(指数函数、对数函数、二次函数、三角函数的图象),直接比较大小。
④中介值法:先把要比较的代数式中间量比较(如“0”“1”),然后再比较它们的大小
2.均值不等式:两个数的算术平均数不小于它们的几何平均数。
若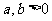 ,则
,则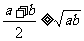 (当且仅当
(当且仅当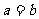 时取等号)
时取等号)
基本变形:① ;
;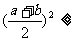 ;
;
②若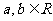 ,则
,则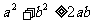 ,
,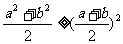
基本应用:①放缩,变形;
②求函数最值:注意:①一正二定三取等;②积定和小,和定积大。
当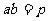 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
当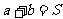 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
常用的方法为:拆、凑、平方;
3.绝对值不等式:



注意:上述等号“=”成立的条件;
4.常用的基本不等式:
(1)设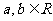 ,则
,则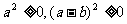 (当且仅当
时取等号)
(当且仅当
时取等号)
(2) (当且仅当 时取等号);
(当且仅当 时取等号); (当且仅 时取等号)
(当且仅 时取等号)
(3)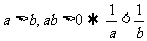 ;
;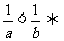 ;
;
4.[答案]观察计算
(1)a+2;(2)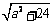 .
.
探索归纳
(1)①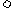 ;②
;②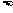 ;
;
(2)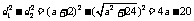 .
.
①当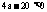 ,即
,即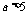 时,
时,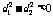 ,
,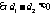 .
.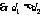 ;
;
②当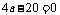 ,即
,即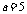 时,
时,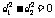 ,
,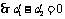 .
.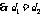 ;
;
③当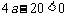 ,即
,即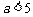 时,
时,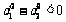 ,
,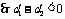 .
.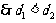 .
.
综上可知:当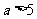 时,选方案二;
时,选方案二;
当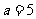 时,选方案一或方案二;
时,选方案一或方案二;
当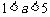 时,选方案一.
时,选方案一.
3.[解析]根据题目中存在的等量关系,容易填写出未知的量,然后建立w与x之间的函数关系式.
[答案]解:(1)填表

依题意得: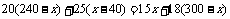 .
.
解得: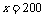 .
.
(2) w与x之间的函数关系为: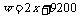 .
.
依题意得: ,∴40≤
,∴40≤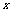 ≤240
≤240
在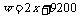 中,∵2>0,∴
中,∵2>0,∴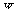 随
随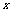 的增大而增大,
的增大而增大,
故当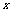 =40时,总运费最小,
=40时,总运费最小,
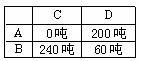
此时调运方案为如下表.
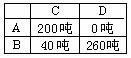
(3)由题意知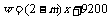
∴0<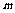 <2时,(2)中调运方案总运费最小;
<2时,(2)中调运方案总运费最小;
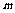 =2时,在40≤
=2时,在40≤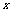 ≤240的前提下调运,方案的总运费不变;
≤240的前提下调运,方案的总运费不变;
2<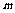 <15时,
<15时, =240总运费最小,
=240总运费最小,
其调运方案如下表
2.[答案]解:(1) 四边形EFGH是正方形.
图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,故CE=CF =CG.∴△CEF是等腰直角三角形.因此四边形EFGH是正方形.
(2)设CE=x, 则BE=0.4-x,每块地砖的费用为y,那么
y=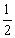 x
x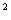 ×30+
×30+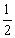 ×0.4×(0.4-x)×20+[0.16-
×0.4×(0.4-x)×20+[0.16-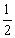 x
x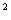 -
-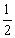 ×0.4×(0.4-x)×10] =10(x
×0.4×(0.4-x)×10] =10(x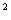 -0.2x+0.24)
=10[(x-0.1)2+0.23] (0<x<0.4) .
-0.2x+0.24)
=10[(x-0.1)2+0.23] (0<x<0.4) .
当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.
答:当CE=CF=0.1米时,总费用最省.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com