《精编》P177　　 5、6

2.由1.得{a_n}是等比数列　　 a₁=0.2 ,　　 q=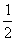

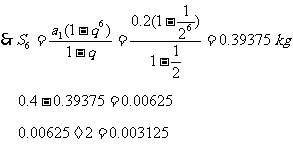
2.经6次倒出后，一共倒出多少k盐？此时加1 kg水后容器内盐水的盐的质量分数为多少？

解：1.每次倒出的盐的质量所成的数列为{a_n}，则：

　　　 a₁= 0.2 kg ,　 a₂=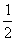×0.2 kg ,　　 a₃= (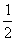)²×0.2 kg

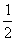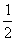　　　 由此可见：a_n= ()^n-1×0.2 kg ,　 a₅= ()^5-1×0.2= (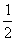)⁴×0.2=0.0125 kg

4．(精编P175 　例3)从盛有盐的质量分数为20%的盐水2 kg的容器中倒出1 kg盐水，然后加入1 kg水，以后每次都倒出1 kg盐水，然后再加入1 kg水，

问：1.第5次倒出的的1 kg盐水中含盐多少g？

3．某城市1991年底人口为500万，人均住房面积为6 m²，如果该城市每年人口平均增长率为1%，每年平均新增住房面积为30万m²，求2000年底该城市人均住房面积为多少m²？(精确到0.01)

解：1991年、1992年、……2000年住房面积总数成AP

　　 a₁ = 6×500 = 3000万m²，d = 30万m²，a₁₀ = 3000 + 9×30 = 3270

1990年、1991年、……2000年人口数成GP

b₁ = 500 , q = 1% ,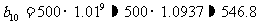　

∴2000年底该城市人均住房面积为：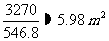

2．在［1000，2000］内能被3整除且被4除余1的整数有多少个？

解：不妨设，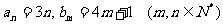

则{c_p}为{ a_n }与{ b_n }的公共项构成的等差数列 (1000≤c_p≤2000)

∵a_n = b_m ,即：3n=4m+1　 　令n=3 , 则m=2　 　∴c₁=9且有上式可知：d=12　

∴c_p=9+12(p-1)　 ( pÎN^*)　

由1000≤c_n≤2000解得：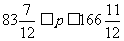　

∴p取84、85、……、166共83项。

1．《教学与测试》P93 例一)大楼共n层，现每层指定一人，共n人集中到设在第k层的临时会议室开会，问k如何确定能使n位参加人员上、下楼梯所走的路程总和最短。(假定相邻两层楼梯长相等)

解：设相邻两层楼梯长为a，则

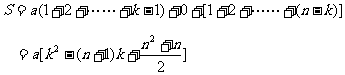
当n为奇数时，取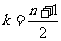　 S达到最小值

当n为偶数时，取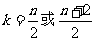　 S达到最大值　

7.今天是星期二，不算今天，2⁵¹天后的第一天是星期几？

6.求91⁹²除以100的余数.

5.用二项式定理证明63⁶³+17能被16整除.