

19.解:(Ⅰ)解: 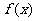 的定义域为
的定义域为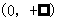 , …..1分
, …..1分
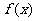 的导数
的导数 . …………..3分
. …………..3分
令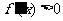 ,解得
,解得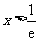 ;令
;令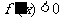 ,解得
,解得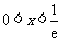 .
.
从而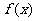 在
在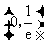 单调递减,在
单调递减,在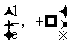 单调递增.
……..5分
单调递增.
……..5分
所以,当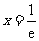 时,
时,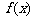 取得最小值
取得最小值 . ……..6分
. ……..6分
(Ⅱ)依题意,得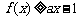 在
在 上恒成立,
上恒成立,
即不等式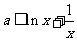 对于
对于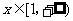 恒成立 . …………..8分
恒成立 . …………..8分
令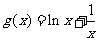 , 则
, 则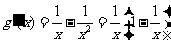 . …………..10分
. …………..10分
当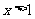 时,因为
时,因为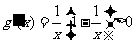 ,
,
故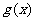 是
是 上的增函数,所以
上的增函数,所以  的最小值是
的最小值是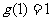 ,
,
从而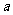 的取值范围是
的取值范围是 .
…………..13分
.
…………..13分
[链接高考]这是一个导数的基本运用考查,考查学生的基本概念的清楚掌握、基本运算的熟练程度,属于容易题,问题的关键在于细心和规范。
18.解:(Ⅰ)∵ED∥PA,则PA∥平面DEFG,而PA 平面APC,
平面APC,
平面DEFG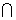 平面APC=FG,∴PA∥FG,
平面APC=FG,∴PA∥FG,
又F为PC的中点,因此G为AC的中点;……………………4分
(Ⅱ)∵点E、D分别AB、PB中点,则∴ED∥PA,且ED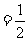 PA,
PA,
同理FG∥PA,且FG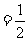 PA,∴ED∥FG,且ED=FG,
PA,∴ED∥FG,且ED=FG,
∴DEFG为平行四边形,由于PA⊥平面ABC,而 ED∥PA,
∴ED⊥平面ABC,∴ED⊥DG,因此DEFG为矩形. ………………9分
(Ⅲ)取PA的中点K,连结KE、KF,则多面体PA-DEFG分成
三棱锥P-KEF和三棱柱KEF-ADG,则多面体PA-DEFG的体积为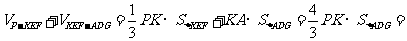
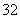 ;
;
多面体BC-DEFG的体积为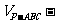
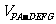 =
=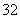 ;………………… 14分
;………………… 14分
17.解:一个人同时转动两个转盘,所得到的数组共有:
(1,1)、(1,2)、(1,3)、(1,4);(2,1)、(2,2)、(2,3)、(2,4);
(3,1)、(3,2)、(3,3)、(3,4);(4,1)、(4,2)、(4,3)、(4,4)共16种…4分
(Ⅰ)若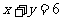 则有(2,4)、(3,3)、(4,2)3种,即
则有(2,4)、(3,3)、(4,2)3种,即
中一等奖的概率为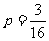 ,
……………………8分
,
……………………8分
(Ⅱ)若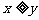 则有(1,1)、(2,1)、(2,2)、(3,1)、(3,2)、(3,3)、(4,1)、(4,2)、(4,3)、(4,4)共10种,即
则有(1,1)、(2,1)、(2,2)、(3,1)、(3,2)、(3,3)、(4,1)、(4,2)、(4,3)、(4,4)共10种,即
中二等奖的概率为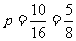 ……………………12分
……………………12分
[链接高考]概率自从2005年走进新高考试题中,就以崭新的姿态,在高考中占有极其重要的地位,每年都有出现,文科主要是用列举法,属于容易题。
16. 解:(Ⅰ)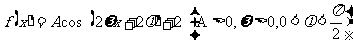 ,
,
依题意 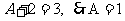 . ……………………1分
. ……………………1分
又  ,
,
 .……………………3分
.……………………3分
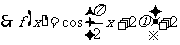 .
.
令 x=0,得 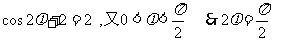 ,
,
所以, 函数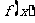 的解析式为
的解析式为 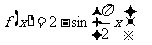 . ……………………6分
. ……………………6分
(Ⅱ)由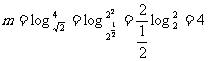 有
有
f(m)+f(m+1)=f(4)+f(5)
=2-sin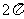 +2-sin
+2-sin =3.
…………………12分
=3.
…………………12分
[链接高考]本小题主要考查三角函数的图象和性质,特殊角的三角函数值,又巧妙与对数结合起来,运用了数形结合等数学思想方法。
(二)选做题(14-15题,考生只能从中选做一题)
14. 2.[解析]曲线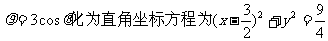 表示圆,直线
表示圆,直线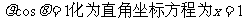 ,由图形知圆心到直线的距离为
,由图形知圆心到直线的距离为 ,所以圆上的点到直线的最大距离为
,所以圆上的点到直线的最大距离为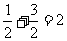 .
.
[链接高考]坐标系与参数方程是选修内容之一,有时考极坐标,有时考参数方程,有时两内容结合一起.
15.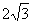 .[解析]由
.[解析]由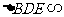
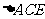 得
得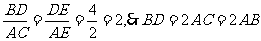 ,在
,在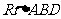 中,AD=6,由勾股定理可求得AB=
中,AD=6,由勾股定理可求得AB=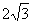 .
.
[链接高考]几何证明选讲中主要有平行成比例、相似三角形、圆中的直径、角、弦、切线等知识.
(一)必做题(11-13题)
11.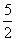 .[解析]第一个输出的数是1;第二个输出的数是
.[解析]第一个输出的数是1;第二个输出的数是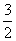 ;第三个输出的数是2;第四个输出的数是
;第三个输出的数是2;第四个输出的数是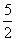 .
.
[链接高考]算法初步是高考新增的考点.近两年每年都有一道小题,常与函数、数列等知识进行小综合来考查,估计以后的考查形式不会有大的变化.
12.3.[解析]复数(2-i)i=1+2i=m+ni(i为虚数单位,m,n为实数),m=1,n=2则m+n=3.
13.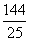 .[解析]画出可行域,由Z=
.[解析]画出可行域,由Z=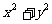 知其几何意义为原点与可行域内点之间的距离平方,从而得到原点到直线4x+3y-12=0的距离为
知其几何意义为原点与可行域内点之间的距离平方,从而得到原点到直线4x+3y-12=0的距离为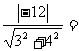
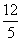 ,z最小值为
,z最小值为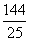
[链接高考]线性规划主要考查动手能力,与其他知识的结合重点在于问题的转化.
10.B.[解析]由三视图可知这几何体是棱长为2的正四面体,它的外接球的直径是棱长为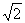 的正方体的对角线
的正方体的对角线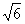 ,球的表面积为
,球的表面积为 .
.
[链接高考]三视图是新增内容,近几年高考都有考,有大题也有小题,立几中正方体是基本的几何模型,要重点掌握.
9.B.[解析]由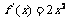
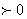 ,得f(x)在(-1,1)上单调递增f(1-x),
,得f(x)在(-1,1)上单调递增f(1-x),
即有 解得
解得 ,故选B.
,故选B.
[链接高考]函数、导数、不等式的综合问题是代数中常见的问题,综合性强,主要考查推理能力.
8. B.[解析]掷甲、乙两颗骰子,总的基本事件有36种,若a=1时,b=2或3;若a=2时,b=1;三种情况满足条件,所以概率为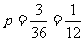 ,故选B.
,故选B.
[链接高考]这是一个典型的古典概型的概率问题, 高考中占有极其重要的地位,近几年高,每年都出现。
7.A.[解析]点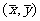 在回归直线上,计算得
在回归直线上,计算得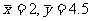 代入得a=2.6.
代入得a=2.6.
[链接高考]统计也是高考新增的考点,07年高考有一大题,不要忘记了。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com