7.[解析]此题为统计与概率知识的综合题,由条形统计图可以判断出三种比赛项目的具体人数,就可以解决第一、二两问.第三问乒乓球门票的价格需要根据统计表中所示的各门票的价格与购买乒乓球门票的总款数占全部门票总款数的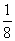,构造方程从而求出乒乓球门票的价格.

[答案](12分)(1)30，20　　

(3)解法一：依题意，有= .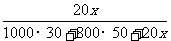　

解得x =500 .　

经检验，x =500是原方程的解.　

答：每张乒乓球门票的价格为500元.　　

解法二：依题意，有= .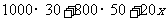

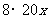解得x =500 .　

答：每张乒乓球门票的价格为500元.　

6.[解析]由图可知点P运动路程在4和9之间时三角形ABP面积不变,说明这时点P在CD边上,因此可知CD=5,BC=4,三角形ABC面积为10

[答案]A

5.[解析]由图象可以知道快艇用时4个小时路程160千米,速度每小时40千米,同样可以得到轮船速度每小时20千米,快艇比轮船晚出发2小时,早到2小时,中间在4小时的时候追上轮船.

[答案]D

4.[解析]按如图这样画n条射线得到的锐角个数为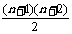

[答案]66

1.[解析]观察图形，第1个图形中“○”的个数为2=1+1；第2个图形中“○”的个数为5=4+1=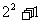；第3个图形中“○”的个数为10=9+1=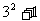；第4个图形中“○”的个数为17=16+1=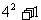；…第n个图形中“○”的个数为.

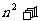[答案]65.

10.(·茂名)我市某工艺厂为配合北京奥运，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：

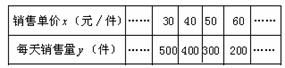
(1)把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；

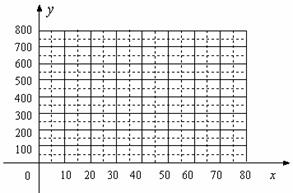(2)当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？(利润=销售总价-成本总价)

(3)当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？

第6课时　 图表信息题　 答案

9.(·恩施自治州)将杨辉三角中的每一个数都换成分数 ，得到一个如图4所示的分数三角形，称莱布尼茨三角形.若用有序实数对(m，n)表示第m行,从左到右第n个数,如(4,3)表示分数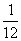.那么(9,2)表示的分数是　　　　　 .

8．(·内江市) 根据图中数字的规律，在最后一个图形中填空．

7.(·龙岩市)下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格，某公司购买的门票种类、数量绘制的条形统计图如下图.

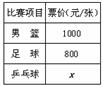
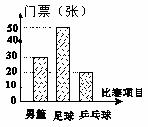
依据上列图、表，回答下列问题：

(1)其中观看男篮比赛的门票有　　　　 张；观看乒乓球比赛的门票占全部门票的　　　 %；

(2)公司决定采用随机抽取的方式把门票分配给100名员工，在看不到门票的条件下，每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀)，问员工小亮抽到足球门票的概率是　　　　　 ；

(3)若购买乒乓球门票的总款数占全部门票总款数的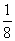，试求每张乒乓球门票的价格.

类型之三　 从表格、数字中寻求规律

能从表格、数字中发现两个量之间存在规律，归纳出相应的关系式.在探索规律的时候，如对于数字问题，可以把等式横向、纵向进行比较，找到其中的数字与其式子的序号之间的关系，然后找到其中的变化规律.