4．　 了解正态分布的意义，能借助正态曲线的图像理解正态曲线的性质。

3．　 　在实际中经常用期望来比较两个类似事件的水平，当水平相近时，再用方差比较两个类似事件的稳定程度。

2．　 了解离散型随机变量的期望值、方差的意义，会根据离散型随机变量的分布列求出期望值、方差

⑴了解随机变量、离散型随机变量的意义，会求出某些简单的离散型随机变量的分布列。 　　 ⑵了解离散型随机变量的期望值、方差的意义，会根据离散型随机变量的分布列求出期望值、方差。 　　 ⑶会用抽机抽样，系统抽样，分层抽样等常用的抽样方法从总体中抽取样本。 　　 ⑷会用样本频率分布去估计总体分布。 　　 ⑸了解正态分布的意义及主要性质。 　　 ⑹了解假设检验的基本思想。 　　 ⑺会根据样本的特征数估计总体。 　　 ⑻了解线性回归的方法。　　　　 三、复习目标

1．　 了解典型分布列：0-1分布，二项分布，几何分布。

离散型随机变量的分布列，离散型随机变量的期望值和平方差，抽样方法，总体分布的估计，正态分布，总体特征数的估计，线性回归。

21．(本题满分16分)

设函数f(x)＝3(1)x³－mx²+(m²－4)x，x∈R．

(1)当m＝3时，求曲线y＝f(x)在点(2，f(2))处的切线方程；

(2)已知函数f(x)有三个互不相同的零点0，α，β，且α＜β．若对任意的x∈[α，β]， 都有f(x)≥f(1)恒成立，求实数m的取值范围．

20．(本题满分13分)

已知：在数列{a_n}中，a₁＝4(1)，a_n+1＝4(1)a_n+4n+1(2)．

(1)令b_n＝4ⁿa_n，求证：数列{b_n}是等差数列；

(2)若S_n为数列{a_n}的前n项的和，S_n+λna_n≥9(5)对任意n∈N^*恒成立，求实数λ的最小值．

19. (本小题满分12)如图，周长为16米的篱笆借助一个墙角围成一个矩形ABCD，在矩形内的一点P处是一棵树，树距离两墙分别为a、4米(0<a<12);若将此树围进去，又使围成的面积最大，如何围法，并求最大面积。　　　　　　　　　　　　

18、 (本小题满分12分)

数列{a_n}的前n项和为S_n，且S_n=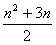。(n∈N*)

　(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若数列{C_n}满足C_n=且{C_n}的前n项和为T_n，求T_2n(n∈N*)

16.　 (本小题满分12分)

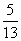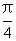已知sinx＝，x∈(，π)，求cos2x和tan(x+)值．

17已知函数。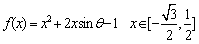

　 (1)当时，求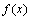的最大值和最小值。

　 (2)若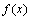在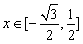上是单调函数，且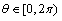，求θ的取值范围。