
2、 《练习册》 P 26 3
四、 小结
用配方法求二次函数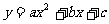 图象的对称轴和顶点坐标公式。
图象的对称轴和顶点坐标公式。
五、 作业
书本 P 55 习题2.5 1
六、 教学后记
1、 书本 P 50 随堂练习
2、 用配方法求二次函数图象的对称轴和顶点坐标
教学重点和难点
重点:用配方法求二次函数图象的对称轴和顶点坐标
难点:用配方法求二次函数图象的对称轴和顶点坐标
教学过程设计
一、 从学生原有的认知结构提出问题
上一节课,我们研究了二次函数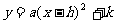 中的a、h、k对二次函数图象的影响。这节课,我们研究一般形式的二次函数图象的作法和性质。
中的a、h、k对二次函数图象的影响。这节课,我们研究一般形式的二次函数图象的作法和性质。
 越大,开口越小;
越大,开口越小; 越小,开口越大
越小,开口越大
当 时,抛物线的开口向上;当
时,抛物线的开口向上;当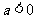 时,抛物线的开口向下;
时,抛物线的开口向下;
当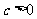 时,抛物线与y轴的交点在原点的上方;当
时,抛物线与y轴的交点在原点的上方;当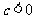 时,抛物线与y轴的交点在原点的下方。
时,抛物线与y轴的交点在原点的下方。
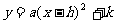 |
开口方向 |
对称轴 |
顶点坐标 |
 |
向上 |
直线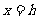 |
(h,k) |
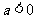 |
向下 |
平移:左加右减 对称轴、顶点坐标:前相反,后相同
二、 师生共同研究形成概念
1、 用配方法求二次函数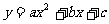 图象的对称轴和顶点坐标
图象的对称轴和顶点坐标
与学生回忆配方的步骤。
2、 讲解例题
例1 用配方法求二次函数图象的对称轴和顶点坐标。
(1)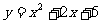 ; (2)
; (2)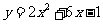 ; (3)
; (3)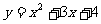 。
。
分析:此处可由老师和学生一起完成,明确配方的步骤。
例2 用配方法求二次函数图象的对称轴和顶点坐标。
(1)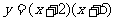 ; (2)
; (2)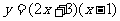 ; (3)
; (3)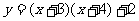 。
。
分析:此例比上一例的难度有所提高,可先学生尝试做,再由老师指导。
三、 随堂练习
1、
经历探索二次函数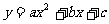 的图象的作法和性质的过程
的图象的作法和性质的过程
答题步骤:
形象类:
(1)找到诗人描绘的形象的有关诗句(2)分析形象的基本含义(3)结合文章主旨分析诗人为什么要写这一形象(4)指出描绘形象的作用或效果。
意境类:
(1)找出诗中的物象,意象(2)展开联想和想象,用自己的语言再现画面,再现画面时既要忠于原诗,又要力求语言优美(3)点明景物所营造的氛围特点。(4)分析表达了诗人怎样的思想感情,或给人什么样的启示和思考。切忌空洞,要答具体。比如光答“表达了作者哀伤的情怀”是不够的,还应答出为什么而“哀伤”。
例析:
西楼
曾巩
海浪如云去却回,
北风吹起数声雷。
朱楼四面钩疏箔,
卧看千山急雨来。
[注]钩疏箔:把帘子挂起。
问:这首诗描写了什么景象?这首诗表达了什么诗人怎样的情感?请简析之。(6分)
答:连天的海浪伴随着阵阵雷声汹涌而来,在北风的呼啸中波浪不断拍打堤岸,又咆哮着远去,这首诗描写了海滨暴风雨来临前的壮美景象,渲染了“山雨欲来风满楼”的雄伟气势。表达了诗人开阔的胸襟和内心豪情。暴风雨将临,按常理本当关门闭户躲避,但诗人却反而高挂起帘子,敞开窗户,为的是能饱览“千山急雨来”的壮观。
附相关术语:常见意象
①以冰雪的晶莹比喻心志的忠贞、品格的高尚。
②对月思亲--引发离愁别绪,思乡之愁。
③以折柳表惜别。“柳”,“留”的谐音,折柳有相留之意。故古人有折柳送别的习俗,因此“柳”带有伤离别的意味。
④以蝉喻品行高洁。古人认为蝉餐风饮露,是高洁的象征。
⑤以草木繁盛反衬荒凉,以抒发盛衰兴亡的感慨。
⑥菊花--坚贞高洁的品质
⑦梅花--傲霜斗雪,不怕打击挫折,纯净洁白
⑧松--坚贞高洁
⑨莲--表达爱情
⑩梧桐--凄凉悲伤的象征
11杜鹃鸟--凄凉哀伤的象征,古代神话中,蜀王杜宇(即望帝)因被迫让位给他的臣子,自己隐居山林,死后灵魂化为杜鹃。于是古诗中的杜鹃也就成为凄凉、哀伤的象征了。
12鹧鸪鸟--离愁别绪
13鸿雁--游子思乡怀亲之情和羁旅伤感,鸿雁是大型候鸟,每年秋季南迁,常常引起游子思乡怀亲之情和羁旅伤感。
在诗歌中,以景传情达意的往往具有一定的固定性,如:以“故乡明月”传达“乡思情”;以“松风山月”传达“隐逸情”;以“寒林残月”传达“诗人的忧愁”;以“中秋圆月”传达“相思情苦”;以“风雨落花,双燕孤飞,重阁玉枕”传达“闺怨情”;以“长亭折柳”传达“惜别情”;以“江湖扁舟,月落乌啼”传达“诗人的羁旅之苦”;以“梦后酒醒,烟柳断肠,寒雨斜阳,残烛啼鹃”传达“悲欢离合情”;以“昔荣今非,几度夕阳红”传达“对世事沧桑的感叹”;以“空城落花”传达“对国势衰危的哀叹、一腔的爱国情”;等等。
[复习教(学)案]鉴赏复习解题指导-情感主旨类
(一)形象意境类
名词解释:
形象――形象理解和分析,是诗歌鉴赏的要点。诗歌中的形象包括事象、物象、意象(事象物象以特定的情意构成了固定的关系)等,既是指叙事诗中的人物形象,也指抒情诗中的抒情主人公,更多的则是指诗歌中所描写的景与物。比如湖光山色、田园桑麻、大漠孤城之类,都是诗歌中的形象。诗歌中的形象倾注着诗人的思想和情感,因此只有真正理解了诗歌的形象,才能深入领会诗歌的思想感情。
意境――意境是诗中意与境两个因素的和谐统一。意是诗人在诗中抒发的思想感情,境是诗中所描绘的艺术图景。所谓意境,就是诗人要表达的思想感情与诗中所描绘的生活图景有机融合而形成的一种耐人寻味的艺术境界。
考查方向:1. 对抒情主体形象的认知理解
2. 对诗歌意象的识别理解
3、对诗歌意境的体味(色彩、构成、情味等)
题目类型:
1.“╳╳的寓意是什么”,“╳╳指什么”,“╳╳在诗中是什么意思”等。
2.“表现了怎样的情景”,“表达了什么意思”,“营造了怎样的气氛”,“塑造了怎样的形象”,“景物有什么特点”等。
3、这首诗歌营造了一个怎样的意境氛围?表达了作者怎样的思想感情?变体:这首诗歌为我们展现了一幅怎样的画面?表达了诗人什么样的思想?这首诗歌描写了什么样的景物?抒发了诗人怎样的情怀?
解题格式:
1、人物形象:身份+性格
2、诗歌意象、含义:表层含义+深层含义(即解释诗句)
3、体会意境:客观形象图景+主观感受+交融了什么意境。
答题要领:可分为三个部分:
分析形象含义、描摹诗歌图景; 概括形象意境特点; 剖析作者思想
[解题技巧]答题格式类型
1.先观点后理由,解题时先表明观点,再陈述理由。
2.先分后总式,答题时,先分说后总
3.先总后分式,答题时,先总说后分说。
4.分点作答式,答题时,分成几点,列出答案。
[解题技巧]分类解析:
不管题干有没有问这方面的问题,这一思考步骤是少不了的。因为它是解答其他鉴赏问题的前提和入门。如果是比较熟悉的诗人的作品,还须知人论世:通过诗人的生平和诗风,类推诗人作品的思想内容、艺术特色和所反映的社会生活。
例1. 2000年全国高考天津理科卷(13)
|
x |
0 |
1 |
2 |
|
p |
|
|
|
某厂生产电子元件,其产品的次品率为5%,现从一批产品中任意连续取出2件,其中次品数x 的概率分布是
解:大批产品中抽取产品,认为次品数x 服从二项分布B(2, 0.05)
空格中应填 0.9025, 0.095, 0.0025
考点:离散型随机变量的概率分布,二项分布
例2. 2001年全国高考天津理科卷(14)
一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出两个,则其中含红球个数的数学期望是__________________.
解1:同时取出的两个球中含红球数 x 的概率分布为
P(x = 0) =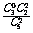 =
=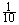 , P(x = 1) =
, P(x = 1) =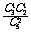 =
=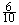 , P(x = 2) =
, P(x = 2) =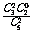 =
=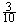
Ex =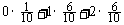 =
=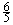 , 空格中应填
, 空格中应填 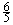
解2:同时取出的两个球中含红球数 x 服从超几何分布,其数学期望为 n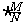 =
=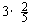 =
=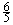
例3. 2002年全国高考天津文科卷(15)
甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t / hm2)
|
品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
|
甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
|
乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
其中产量比较稳定的小麦品种是 甲 。
提示:¯甲 = 1 5( 9.8 + 9.9 + 10.1 + 10 + 10.2) = 10.0,¯乙 = 1 5( 9.4 + 10.3 + 10.8 + 9.7 + 9.8) = 10.0;
s 2甲 = 1 5( 9.82 + … + 10.22) – 102 = 0.02,s 2甲 = 1 5( 9.42 + … + 9.82) – 102 = 0.244 > 0.02 。
例4. 2003年全国高考江苏卷(14) 辽宁卷(14) 天津文科卷(14) 天津理科卷(14)
某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆。为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取 6 ,z 30 , 10 辆。
提示:1200 + 6000 + 2000 = 9200;46 : 9200 = 1 : 20;
\ 1200 ´ 1 20 = 6,6000 ´ 1 20 = 30,2000 ´ 1 20 = 10。
例5. 抽样本检查是产品检查的常用方法.分为返回抽样和不返回抽样两种具体操作方案.现有100只外型相同的电路板,其中有40只A类版后60只B类板.问在下列两种情况中“从100只抽出3只,3只都是B类”的概率是多少?
⑴ 每次取出一只,测试后放回,然后再随机抽取下一只(称为返回抽样);
⑵ 每次取出一只,测试后不放回,在其余的电路板中,随意取下一只(称为不返回抽样)
解:⑴ 设“从100只中抽去3只,3只都是B类”为事件M,先求基本事件总数,由于每次抽去一只,测试后又放回,故每次都是从100只电路板中任取一只,这是重复排列,共有
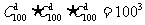 个.再求M所包含的基本事件数,由于每次抽出后又放回,故是重复排列,共有
个.再求M所包含的基本事件数,由于每次抽出后又放回,故是重复排列,共有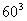 个,所以
个,所以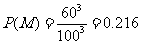
⑵ 由于取出后不放回,所以总的基本事件数为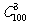 个,事件M的基本事件数为
个,事件M的基本事件数为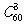 ,所以
,所以 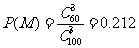
例6. 已知连续型随机变量ε的概率密度函数 ,且f(x) ≥0,求常数k的值,并计算概率P(1.5≤ε<2.5)。
,且f(x) ≥0,求常数k的值,并计算概率P(1.5≤ε<2.5)。
分析:凡是计算连续型随机变量ε的密度函数f(x)中的参数、概率P(a≤ε≤b)都需要通过求面积来转化而求得。若f(x) ≥0且在[a,b]上为线性,那么P(a≤ε≤b)的值等于以b-a为高,f(a)与f(b)为上、下底的直角梯形的面积,即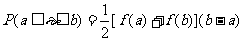 。
。
解: ∵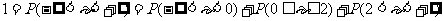
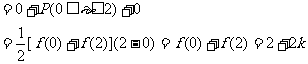
∴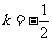 ;
;
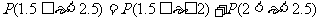
例7. 对划艇运动员甲、乙二人在相同的条件下进行了6次测试,测得他们最大速度的数据如下:
甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36。
根据以上数据,试判断他们谁更优秀。
分析:根据统计知识可知,需要计算两组数据的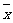 与
与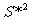 ,然后加以比较,最后再作出判断。
,然后加以比较,最后再作出判断。
解: 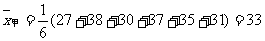 ,
,
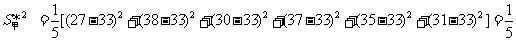
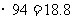 ;
;
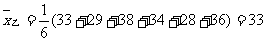 ,
,
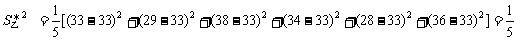
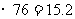
∴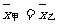 ,
, ,
,
由此可以说明,甲、乙二人的最大速度的平均值相同,但乙比甲更稳定,故乙比甲更优秀。
说明: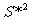 与
与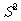 作为总体方差的两个估计量,当样品容量不是很大时,
作为总体方差的两个估计量,当样品容量不是很大时,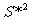 更接近
更接近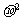 ,故在实际运用时,我们常用
,故在实际运用时,我们常用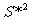 去估计
去估计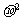 ,但当容量较大时,
,但当容量较大时,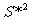 与
与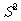 则没有什么差别。
则没有什么差别。
例8.几何分布
某射击手击中目标的概率为P。求从射击开始到击中目标所需次数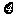 的期望、方差。
的期望、方差。
解:
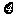 |
1 |
2 |
3 |
…… |
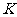 |
…… |
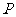 |
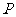 |
 |
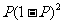 |
|
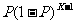 |
|
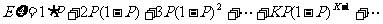
令
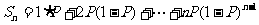
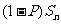
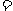


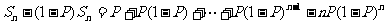
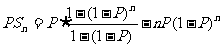
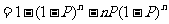
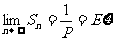
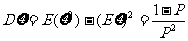
例9.设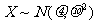 ,且总体密度曲线的函数表达式为:
,且总体密度曲线的函数表达式为:
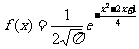 ,x∈R。
,x∈R。
(1)求μ,σ;(2)求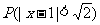 及
及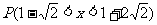 的值。
的值。
分析:根据表示正态曲线函数的结构特征,对照已知函数求出μ和σ。利用一般正态总体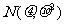 与标准正态总体N(0,1)概率间的关系,将一般正态总体划归为标准正态总体来解决。
与标准正态总体N(0,1)概率间的关系,将一般正态总体划归为标准正态总体来解决。
解: (1)由于 ,根据一般正态分布的函数表达形式,可知μ=1,
,根据一般正态分布的函数表达形式,可知μ=1,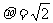 ,故X-N(1,2)。
,故X-N(1,2)。
(2)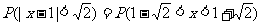
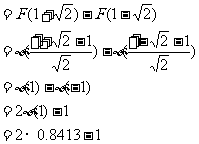
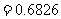 。
。
又

 。
。
说明:在解决数学问题的过程中,将未知的,不熟悉的问题转化为已知的、熟悉的、已解决了的问题,是我们常用的手段与思考问题的出发点。通过本例我们还可以看出一般正态分布与标准正态分布间的内在关联。
例10.公共汽车门的高度是按照确保99%以上的成年男子头部不跟车门顶部碰撞设计的,如果某地成年男子的身高ε-N(173,7)(单位:cm),问车门应设计多高(精确到1cm)?
分析:由题意可知,求的是车门的最低高度,可设其为xcm,使其总体在不低于x的概率小于1%。
解:设该地区公共汽车车门的最低高度应设为xcm,由题意,需使P(ε≥x)<1%。
∵ε-N(173,7),∴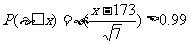 。查表得
。查表得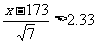 ,解得x>179.16,即公共汽车门的高度至少应设计为180cm,可确保99%以上的成年男子头部不跟车门顶部碰撞。
,解得x>179.16,即公共汽车门的高度至少应设计为180cm,可确保99%以上的成年男子头部不跟车门顶部碰撞。
说明:解决本题的关键是在正确理解题意的基础上,找出正确的数学表达式;而逆向思维和逆向查表,体现解决问题时思维的灵活性。
例11.已知某地每单位面积菜地年平均使用氮肥量xkg与每单位面积蔬菜年平均产量yt之间的关系有如下数据:
|
年份 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
|
x(kg) |
70 |
74 |
80 |
78 |
85 |
92 |
90 |
95 |
|
y(t) |
5.1 |
6.0 |
6.8 |
7.8 |
9.0 |
10.2 |
10.0 |
12.0 |
|
年份 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
x(kg) |
92 |
108 |
115 |
123 |
130 |
138 |
145 |
|
y(t) |
11.5 |
11.0 |
11.8 |
12.2 |
12.5 |
12.8 |
13.0 |
(1)求x与y之间的相关系数,并检验是否线性相关;
(2)若线性相关,求蔬菜产量y与使用氮肥量之间的回归直线方程,并估计每单位面积施肥150kg时,每单位面积蔬菜的年平均产量。
分析:(1)使用样本相关系数计算公式来完成;(2)查表得出显著性水平0.05与自由度15-2相应的相关系数临界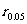 比较,若
比较,若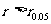 则线性相关,否则不线性相关。
则线性相关,否则不线性相关。
解:(1)列出下表,并用科学计算器进行有关计算:]
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
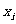 |
70 |
74 |
80 |
78 |
85 |
92 |
90 |
95 |
92 |
108 |
115 |
123 |
130 |
138 |
145 |
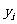 |
5.1 |
6.0 |
6.8 |
7.8 |
9.0 |
10.2 |
10.0 |
12.0 |
11.5 |
11.0 |
11.8 |
12.2 |
12.5 |
12.8 |
13.0 |
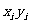 |
357 |
444 |
544 |
608.4 |
765 |
938.4 |
900 |
1140 |
1058 |
1188 |
1357 |
1500.6 |
1625 |
1766.4 |
1885 |
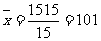 ,
,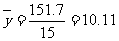 ,
,
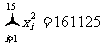 ,
,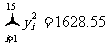 ,
, 。故蔬菜产量与放用氮肥量的相关系数
。故蔬菜产量与放用氮肥量的相关系数
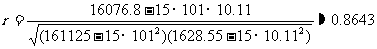 。
。
由于n=15,故自由度15-2=13。由相关系数检验的临界值表查出与显著水平0.05及自由度13相关系数临界值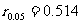 ,则
,则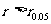 ,从而说明蔬菜产量与氮肥量之间存在着线性相关关系。
,从而说明蔬菜产量与氮肥量之间存在着线性相关关系。
(2)设所求的回归直线方程为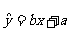 ,则
,则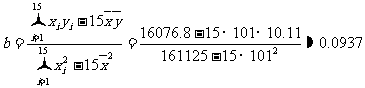 ,
,
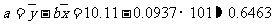 ,
,
∴回归直线方程为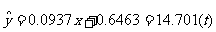 。
。
说明:求解两个变量的相关系数及它们的回归直线方程的计算量较大,需要细心、谨慎地计算。如果会使用含统计的科学计算器,能简单得到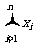 ,
, ,
,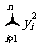 ,
,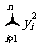 ,
,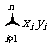 这些量,也就无需有制表这一步,直接算出结果就行了。另外,利用计算机中有关应用程序也可以对这些数据进行处理。
这些量,也就无需有制表这一步,直接算出结果就行了。另外,利用计算机中有关应用程序也可以对这些数据进行处理。
例12.设随机变量ε服从N(0,1),求下列各式的值:
(1)P(ε≥2.55); (2)P(ε<-1.44); (3)P(|ε|<1.52)。
分析:一个随机变量若服从标准正态分布,可以借助于标准正态分布表,查出其值。但在标准正态分布表中只给出了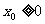 ,即
,即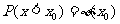 的情形,对于其它情形一般用公式:φ(-x)=1-φ(x);p(a<x<b)=
φ(b)- φ(a)及
的情形,对于其它情形一般用公式:φ(-x)=1-φ(x);p(a<x<b)=
φ(b)- φ(a)及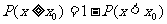 等来转化。
等来转化。
解:(1)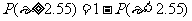
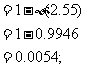
(2)
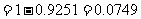 ;
;
(3)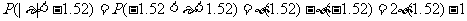

说明:从本题可知,在标准正态分布表中只要给出了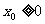 的概率,就可以利用上述三个公式求出其它情形下的概率。
的概率,就可以利用上述三个公式求出其它情形下的概率。
例13.某厂生产的圆柱形零件的外径ε-N(4,0.25)。质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外径为5.7cm。试问该厂生产的这批零件是否合格?
分析:欲判定这批零件是否合格,由假设检验基本思想可知,关键是看随机抽查的一件产品的尺寸是在(μ-3σ,μ+3σ)内,还是在(μ-3σ,μ+3σ)之外。
解:由于圆柱形零件的外径ε-N(4,0.25),由正态分布的特征可知,正态分布N(4,0.25)在区间(4-3×0.5,4+3×0.5)即(2.5,5.5)之外取值的概率只有0.003,而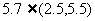 ,这说明在一次试验中,出现了几乎不可能发生的小概率事件,根据统计中假设检验的基本思想,认为该厂这批产品是不合格的。
,这说明在一次试验中,出现了几乎不可能发生的小概率事件,根据统计中假设检验的基本思想,认为该厂这批产品是不合格的。
说明:判断某批产品是否合格,主要运用统计中假设检验的基本思想。
例14.假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
|
x |
2 |
3 |
4 |
5 |
6 |
|
y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知y对x呈线性相关关系。试求:
(1)线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
分析:本题为了降低难度,告诉了y与x间呈线性相关关系,目的是训练公式的使用。
解:(1)列表如下:
|
i |
1 |
2 |
3 |
4 |
5 |
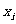 |
2 |
3 |
4 |
5 |
6 |
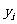 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
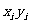 |
4.4 |
11.4 |
22.0 |
32.5 |
42.0 |
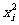 |
4 |
9 |
16 |
25 |
36 |
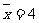 , ,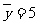  , ,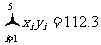 |
于是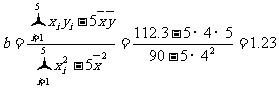 ,
,
 。
。
∴线性回归方程为: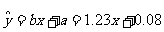 。
。
(2)当x=10时,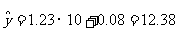 (万元)
(万元)
即估计使用10年时维修费用是12.38万元。
说明:本题若没有告诉我们y与x间是呈线性相关的,应首先进行相关性检验。如果本身两个变量不具备线性相关关系,或者说它们之间相关关系不显著时,即使求出回归方程也是没有意义的,而且其估计与预测也是不可信的。
例15. (2003年全国高考辽宁卷(20) 天津理科卷(20))
A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3 。按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
2 3 |
1 3 |
|
A2对B2 |
2 5 |
3 5 |
|
A3对B3 |
2 5 |
3 5 |
现按表中对阵方式出场, 每场胜队得1分, 负队得0分。设A队、B队最后总分分别为 x、h。
(Ⅰ) 求 x、h 的概率分布;
(Ⅱ) 求Ex、Eh。
分析:本题考查离散型随机变量分布列和数学期望等概念,考查运用概率知识解决实际问题的能力。
解:(Ⅰ) x、h 的可能取值分别为3, 2, 1, 0.
P(x = 3) =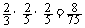 (即A队连胜3场)
(即A队连胜3场)
P(x = 2) =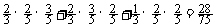 (即A队共胜2场)
(即A队共胜2场)
P(x = 1) =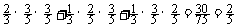 (即A队恰胜1场)
(即A队恰胜1场)
P(x = 0) =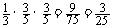 (即A队连负3场)
(即A队连负3场)
根据题意知 x + h = 3,所以
P(h = 0) = P(x = 3) = 8 75, P(h = 1) = P(x = 2) = 28 75,
P(h = 2) = P(x = 1) = 2 5, P(h = 3) = P(x = 0) = 3 25 。
(Ⅱ) Ex =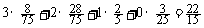 ;
;
因为x + h = 3,
所以Eh = 3 – Ex =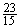 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com