
1.重点:双曲线的定义和双曲线的标准方程.
(解决办法:通过一个简单实验得出双曲线,再通过设问给出双曲线的定义;对于双曲线的标准方程通过比较加深认识.)
(三)学科渗透点
本次课注意发挥类比和设想的作用,与椭圆进行类比、设想,使学生得到关于双曲线的定义、标准方程一个比较深刻的认识.
(二)能力训练点
在与椭圆的类比中获得双曲线的知识,从而培养学生分析、归纳、推理等能力.
(一)知识教学点
使学生掌握双曲线的定义和标准方程,以及标准方程的推导.
通过对向量数量积的定义的理解,我们初步掌握向量数量积的几何意义,重要性质及运算律。
1) 计算向量数量积,向量的模,向量的夹角。
2) 判断向量的位置关系(特别是垂直关系)。
3) 向量的运算律的运用。
例1.判断正误,并简要说明理由.
(1)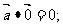
(2) 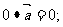
(3)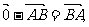
(4)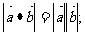
(5)若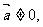 则对任一非零
则对任一非零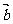 有
有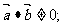
(6)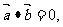 则
则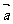 与
与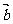 中至少有一个为0;
中至少有一个为0;
(7)对任意向量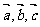 都有
都有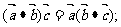
(8) 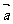 与
与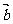 是两个单位向量,则
是两个单位向量,则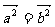 .
.
例2已知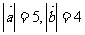
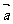 与
与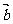 的夹角
的夹角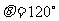 ,求
,求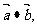
变式1:已知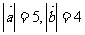 ,
,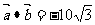 ,求
,求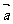 与
与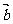 的夹角。
的夹角。
变式2:已知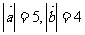 ,
,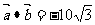 ,求
,求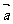 在
在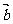 上的投影。(引申:夹角为
上的投影。(引申:夹角为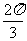 时投影为负,那么夹角为
时投影为负,那么夹角为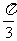 时投影为?投影是有正负的,与我们初中学的射影不同)
时投影为?投影是有正负的,与我们初中学的射影不同)
变式3:已知在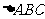 中,
中,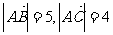 ,
,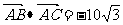 ,求
,求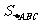
变式4:已知在等边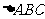 中,
中,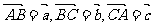 ,则
,则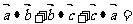
例3求证:
1)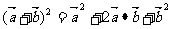
2)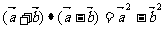
例4已知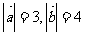 (且
(且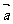 与
与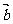 不共线),当且仅当
不共线),当且仅当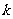 为何值时,向量
为何值时,向量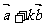 与
与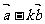 互相垂直?
互相垂直?
1. 数量积的运算律
已知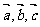 和实数
和实数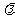 ,则向量的数量积满足下列运算律:
,则向量的数量积满足下列运算律:
(1)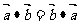 (交换律)
(交换律)
(2)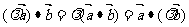 (数乘结合律)
(数乘结合律)
(3)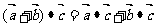 (分配律)
(分配律)
说明:(1)一般地,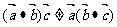 向量的数量积不满足结合律
向量的数量积不满足结合律
(2) 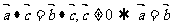 “实数a,b,c,且ab=ac,a
“实数a,b,c,且ab=ac,a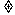 0推出b=c”
0推出b=c”
(3)有如下常用性质:
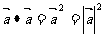 ,
,
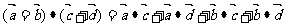 ,
,
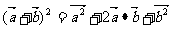
4.数量积的重要性质
设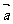 与
与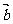 都是非零向量,
都是非零向量,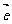 是单位向量,
是单位向量,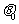 是
是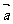 与
与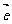 夹角,
夹角, 是
是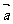 与
与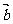 夹角.
夹角.
(1)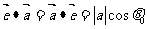
(2)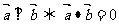
(3)当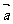 与
与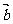 同向时,
同向时,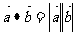
当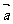 与
与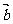 反向时,
反向时, 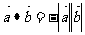
特别地,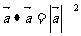 或
或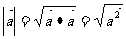
(4)cos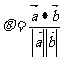
(5)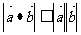
说明:上述性质要求学生结合数量积的定义自己尝试推导.
3.数量积的几何意义
两个向量的数量积等于其中一个向量的长度与另一个向量在其上的投影值的乘积.
说明:这个投影值可正可负也可为零,所以我们说向量的数量积的结果是一个实数.
2.数量积的定义
已知两个非零向量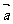 与
与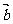 ,它们的夹角是
,它们的夹角是 ,则数量
,则数量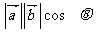 .叫
.叫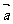 与
与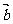 的数量积,记作
的数量积,记作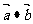 ,即有
,即有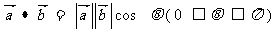
说明:(1)零向量与任一向量的数量积为0,即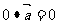 ;
;
(2)符号“ ”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com