
7. 化简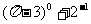 的结果为:
的结果为:
A. 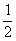 B.
-2 C.
B.
-2 C.  D.
D.
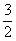
6. 若a<0,代简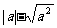 的结果正确的是_________
的结果正确的是_________
A. 0 B. 2a C. -2a D. 2a或-2a
5. 已知 ,(其中x≠0,m、n为正整数),则
,(其中x≠0,m、n为正整数),则 的值等于______
的值等于______
A.  B.
B.
 C.
C.
 D.
D.

4. 如果2(x+3)的值与3(1-x)的值互为相反数,那么x等于_________
A. 9 B. 2 C. 3 D. 4
3. 一天的时间共86400秒,用科学记数法表示应为_________
A.  B.
B. 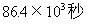 C.
C.  D.
D.
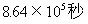
2. 设a,b为两实数,则下列命题中是假命题的是_________
A. 若a+b=0,则|a|=|b| B. 若|a|+|b|=0,则a=b=0
C. 若a2+b2=0,则a=b=0 D. 若|a+b|=0,则a=b=0
1. 下列各组数中,相等的是_________
A. 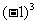 和1 B.
和1 B.  和-1 C.
和-1 C. 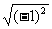 和-1 D.
和-1 D.

(五)代数式的化简求值
含有绝对值的代数式的化简,通常可利用数轴的直观性;整式的化简求值常常要灵活运用配方法、换元法、整体代换思想和构造思想;分式的化简求值一般可对分子、分母的多项式因式分解、约分。再运用分式的性质化简计算;二次根式的化简求值一般应先考虑能否利用二次根式的性质,配方法、乘法公式等化简计算。
[典型例题]
例1. 在
A. 1 B. 2 C. 3 D. 4
分析:应当知道,只有无限不循环的小数才是无理数,有限小数0.80108,无限循环小


例2. 已知下列5个命题
(1)零是最小的实数
(2)数轴上所有的点都表示实数
(3)两个无理数的和仍然是无理数
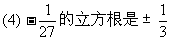
(5)任何实数都有两个互为相反数的平方根
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
分析:(1)要正确区分实数的最小值和实数绝对值最小值的意义
(2)要正确区分平方根和立方根的相同点和不同点
(3)“任何数……”就意味着没有例外,因此若能举出一个反例便可证明原命题是假命题。
因此可以得出5个命题中只有(2)是真命题,故选A。
例3. 
解: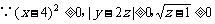



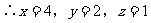

注意:这是一个条件求值问题,利用非负数的性质可以求出x、y、z的值,从而使问题得解。
例4. 
解:



归纳:
其中a≠0,P是正整数,在本题中,


例5. 
的值为( )
解: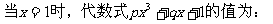



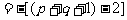

例6. 
解: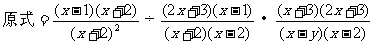
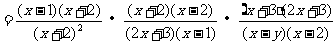

归纳:对分子、分母都是多项式的分式进行乘除运算时,一定要先将每个多项式分解因式,然后将除法统一成乘法,最后再进行约分化简。
实战演练
(四)代数式的恒等变形
添括号、去括号、拆项是代数式恒等变形的常用方法,乘法公式、因式分解是代数式恒等变形的工具。待定系数法、配方法也都可进行代数式的恒等变形。
(三)和代数式有关的概念及代数式的运算。
(1)代数式的分类

(2)各类代数式的概念
单项式、多项式、整式、分式、有理式、无理式、根式、二次根式、最简二次根式、同类二次根式。
(3)代数式有意义的条件:
分式有意义的条件是分母不为零
分式的值为零的条件是分母不为零,分子为零二次根式有意义的条件是被开方数(式)非负,由实际应用中得到的代数式还要符合实际意义。
(4)代数式的运算:
整式的加、减、乘、除运算及添括号、去括号法则。
分式的加、减、乘、除运算及分式的乘方。
二次根式的加、减、乘、除运算及二次根式的分母有理化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com