
1.我国的人民代表大会制度与西方的议会共和制、总统制同属于民主共和制,但两者有不同之处,这种不同从本质上说在于 ( )
A.所体现的阶级属性不同 B.所体现的国家结构不同
C.所体现的权力授受关系不同 D.所体现的国家政权运行方式不同
14. 设函数 ,当点
,当点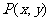 是函数
是函数 图像上的点,则点
图像上的点,则点 是函数
是函数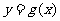 图像上的点.
图像上的点.
(1)求 ; (2)若当
; (2)若当 是,恒有
是,恒有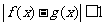 ,试确定
,试确定 的取值范围 .
的取值范围 .
|loga(x-3a)+loga(x-a)|≤1,x>3a,即-1≤loga(x2-4ax+3a2)≤1. 由3a<a+2及a>0,
|
 ,即
,即
解不等式①,得 或
或 .
.
由题设知[a+2,a+3]
 ,
,
∴ 或
或 结合0<a<1,解得
结合0<a<1,解得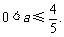
对于不等式②,令h(x)=x2-4ax+3a2- ,则[a+2,a+3]是不等式h(x)≤0的解集的子集的充要条件是
,则[a+2,a+3]是不等式h(x)≤0的解集的子集的充要条件是 结合0<a<1,解得
结合0<a<1,解得
综上所述,存在 ,使得当x∈[a+2,a+3]时,不等式
,使得当x∈[a+2,a+3]时,不等式 恒成立.
恒成立.
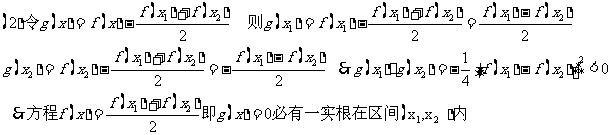
13. 已知二次函数 ,
,
(1)
若 且
且 ,证明:
,证明: 的图像与x轴有两个相异交点;
的图像与x轴有两个相异交点;
(2)
若 ,且
,且 .证明:方程
.证明:方程 必有一实根在区间
必有一实根在区间  内;
内;
(3)
在(1)的条件下,设两交点为 ,求线段
,求线段 长的取值范围 .
长的取值范围 .


12. 已知定义在 上的减函数
上的减函数 ,满足条件:对任意实数
,满足条件:对任意实数 都有
都有 =
= .
.
(1)求 的值; (2)根据函数奇偶性的定义,证明:
的值; (2)根据函数奇偶性的定义,证明: 是奇函数;
是奇函数;
(3)若 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围 .
的取值范围 .
11. 甲、乙两地相距 千米,汽车从甲地匀速行驶到乙地,速度不得超过
千米,汽车从甲地匀速行驶到乙地,速度不得超过 千米/时.已知汽车每小时的运
千米/时.已知汽车每小时的运
输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 (千米/时)的平方成正比,比例
(千米/时)的平方成正比,比例
系数为 ;固定部分为
;固定部分为 元.
元.
(Ⅰ) 全程运输成本把 (元)表示为速度
(元)表示为速度 (千米/时)的函数,并指出这个函数的定义域
;
(千米/时)的函数,并指出这个函数的定义域
;
(Ⅱ) 为了使全程运输成本最小,汽车应以多大速度行驶 ?
 故所求函数
故所求函数  (Ⅱ)依题意知S,a,b,v都为正数,故有
(Ⅱ)依题意知S,a,b,v都为正数,故有 

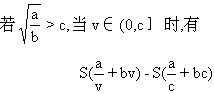
 因为c-v≥0,且a>bc2,故有 a-bcv≥a-bc2>0,
因为c-v≥0,且a>bc2,故有 a-bcv≥a-bc2>0,
 也即当v=c时,全程运输成本y最小.
也即当v=c时,全程运输成本y最小.

10. 若函数 满足
满足 ,且
,且 时,
时, .则
.则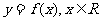 的图象与函数
的图象与函数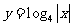 的图象的交点的个数为( C ).
的图象的交点的个数为( C ).
A.3 B.4 C.6 D.8
9. 对于给定函数 ,有下列四个结论:
(1)
,有下列四个结论:
(1) 的图像关于原点对称;
的图像关于原点对称;
(2) 在R上是增函数; (3)
在R上是增函数; (3) ; (4)
; (4)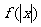 有最小值0.
有最小值0.
其中正确的结论序号是 ____________ .
8.  值域是 .
值域是 .
7. 记 . 若
. 若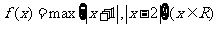 的最小值是( C )
的最小值是( C )
A.0 B. C.
C. D.3
D.3
6. 已知函数 满足:对任意
满足:对任意 ,当
,当 时,
时,
总有 ,那么
,那么 的取值范围是( )
的取值范围是( )
A. B.
B.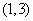 C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com