0．已知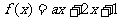，当时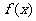，有正值也有负值，则实数a的取值范围为　　　　　　　　　　　　 。

5.[解析]通过计算可以得知整个图形的面积为12，我们只需截出一个面积为6的图形就可以把图形面积一分为二。

4.[解析]由折叠知：∠ADG=∠GDO根据外角定理∠AGD=∠GDO+∠GOD而∠GOD=90°，∠GDO = 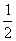∠ADO=22.5°得∠AGD=112.5°所以①正确。由折叠知△AGD≌△FGD得S△AGD=S△FGD所以③错误。∠AED=90°-22.5°=67.5°，∠AGE=45°+22.5°=67.5°故∠AED=∠AGE可得AE=AG，易证AG=FG，AE=EF，从而得AG=FG=AE=EF。所以④正确。BE=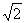EF，EF= FG=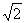OG，故BE=2OG所以⑤正确。AE= FG=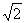OG，AD= AB=AE+ BE=(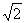+2)OG，在Rt△AED中tan∠AED==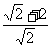，所以②错误。

[答案]①④⑤．

3.[解析]由折叠可知∠BAE=∠CAE，因为AE=EC所以∠CAE=∠ACE，所以∠BAE=∠CAE=∠ACE，三角的和为90°，所以∠ACE=30°，所以AC=2AB=4

[答案]4

2.[解析]本题一方面考查学生的空间想象能力，另一方面还考查学生的动手操作能力。当学生的空间想象受到影响时，可借助动手实践，直接折纸、剪纸，得到答案。答案为D。

[答案]D

1.[解析]本题是折叠、裁减问题，折叠会体现对称，可以动手操作验证。

[答案]C

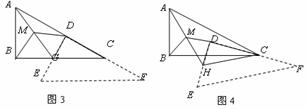
12．(·仙桃市)小华将一张矩形纸片(如图1)沿对角线CA剪开，得到两张三角形纸片(如图2)，其中∠ACB=α，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上.

(1)若ED与BC相交于点G，取AG的中点M，连接MB、MD，当△EFD纸片沿CA方向平移时(如图3)，请你观察、测量MB、MD的长度，猜想并写出MB与MD的数量关系，然后证明你的猜想；

(2)在(1)的条件下，求出∠BMD的大小(用含α的式子表示)，并说明当α=45°时，△BMD是什么三角形？

(3)在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度(旋转角度小于90°)，此时△CGD变成△CHD，同样取AH的中点M，连接MB、MD(如图4)，请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不需要证明，并说明α为何值时，△BMD为等边三角形.

第7课时　 动手操作题　 答案

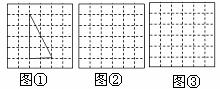
11．(·沈阳市)如图所示，在6×6的方格纸中，每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形，如图①中的三角形是格点三角形．

(1)请你在图①中画一条直线将格点三角形分割成两部分，将这两部分重新拼成两个不同的格点四边形，并将这两个格点四边形分别画在图②，图③中；

(2)直接写出这两个格点四边形的周长．

类型之四　 探索性问题

此类题目常涉及到画图、测量、猜想证明、归纳等问题，它与初中代数、几何均有联系．此类题目对于考查学生注重知识形成的过程，领会研究问题的方法有一定的作用，也符合新课改的教育理念．

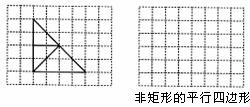
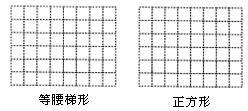
10.(·襄樊市)如图，方格纸中有一透明等腰三角形纸片，按图中裁剪线将这个纸片裁剪成三部分．请你将这三部分小纸片重新分别拼接成；(1)一个非矩形的平行四边形；(2)一个等腰梯形；(3)一个正方形．请在图中画出拼接后的三个图形，要求每张三角形纸片的顶点与小方格顶点重合．

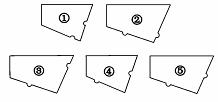
9.(•芜湖市)从下列图中选择四个拼图板，可拼成一个矩形，正确的选择方案为　　　 　． (只填写拼图板的代码)