
4.(06天津)函数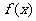 的定义域为开区间
的定义域为开区间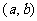 ,导
,导
函数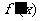 在
在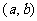 内的图象如图所示,则函数
内的图象如图所示,则函数
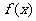 在开区间
在开区间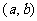 内有极小值点( )
内有极小值点( )
A 1个 B 2个 C 3个 D 4个
3.(06四川)已知 ,下面结论正确的是(
)
,下面结论正确的是(
)
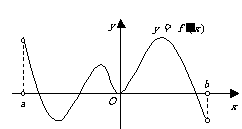 A
A 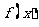 在
在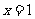 处连续 B
处连续 B 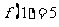 C
C D
D 
2. 数列{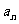 }满足:
}满足: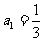 ,且对任意的
,且对任意的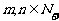 有
有 ,则
,则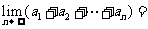 ____
____
1. 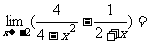 ;
; 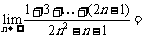 __ ___
__ ___
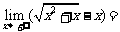 ;
;
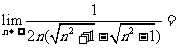 __ ___
__ ___
6. 求可导函数最值的步骤:(1)求出所有的极值点;(2)求出端点出函数值;(3)作比较 .
注:(1)一切应用的基础是:先通过导数判断函数的单调性,再通过单调性研究其他性质 .
(2)关于上凸、下凸函数的最值:
5. 求极值的步骤:求导数;找所有的可疑点(包括导数不存在的点);判定可疑点两侧导数是否变号 .
4. 导数公式: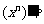 ______;
______;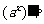 _______,
_______, 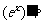 ____;
____;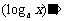 ________,
________, 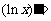 _____;
_____;
 _____,
_____,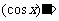 _____;
_____;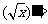 _____,
_____,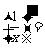 _____;
_____;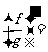 __________.
__________.
3. 导数的定义式(2种): 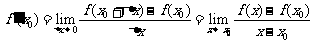 (求极限
(求极限 求导数)
求导数)
2. 连续的定义:在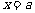 的左、右极限存在且相等 . 注意:可导必连续,连续不一定可导 .
的左、右极限存在且相等 . 注意:可导必连续,连续不一定可导 .
1. 注意极限运算法则的使用前提:极限存在,且对有限个数(式).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com