
1.下列词语中加点的字,读音完全正确的一组是
A.菁华 (qīng) 宁可(nìng) 冠心病(guān) 翘首回望(qiáo)
B.吐蕃(fān) 庇护(bì) 歼击机(jiān) 呱呱坠地(gū)
C.请帖(tiě) 梵文(fán) 发横财(hèng) 按捺不住(nà)
D.链接(liàn) 创口(chuāng) 倒春寒(dào) 拈花惹草(niān)
[答案]D
[考点]考查正确识记现代汉语普通话的字音,能力层级为A级。
[解析]A.菁华(jīng);B.吐蕃(bō);C.梵文(fàn)。
[思路分析]该题每一个选项中加点的字都是常见易读错的字,涉及多音字、形声字、形近字。针对命题特点,只要平时多注意积累,勤查字典,问题就可迎刃而解。其中多音字可以通过记少推多(如“呱呱坠地”仅在此处读gū)、区别口语和书面语或区别词性、词义(如“冠心病”,“冠”,帽子(名词)/“冠军”,第一)。
习题3.5 ①,②,③,④,⑤
再介绍两种推导等比数列求和公式的方法,(作机动)
法1:设
∵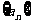 成GP,∴
成GP,∴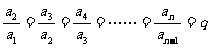
由等比定理: 即:
即: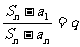
当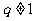 时,
时,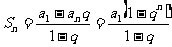
当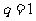 时,
时,
法2: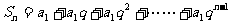
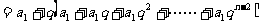
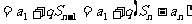
从而: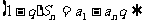 当
当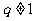 时
时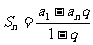 (下略)
(下略)
当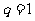 时
时
例2、(P131,例二略)--应用题,且是公式逆用(求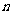 ),要用对数算。
),要用对数算。
例3、(P131-132,例三略)--简单的“分项法”。
例4、设数列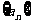 为
为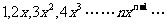
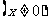 求此数列前
求此数列前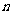 项的和。
项的和。
解:(用错项相消法)  ①
①
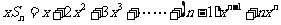 ②
②
①-②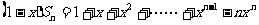 ,
,
当 时,
时,
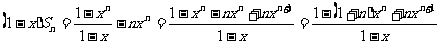
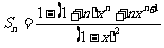
当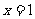 时,
时,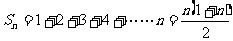
乘以公比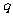 ,
, ②
②
①-②: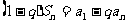 ,
,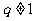 时:
时: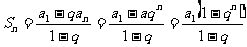
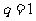 时:
时:
注意:(1)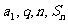 和
和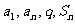 各已知三个可求第四个,
各已知三个可求第四个,
(2)注意求和公式中是 ,通项公式中是
,通项公式中是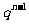 不要混淆,
不要混淆,
(3)应用求和公式时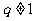 ,必要时应讨论
,必要时应讨论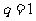 的情况。
的情况。
即求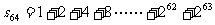 ①
①
用错项相消法推导结果,两边同乘以公比:
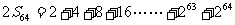 ②
②
②-①: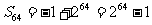 这是一个庞大的数字>1.84×
这是一个庞大的数字>1.84×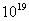 ,
,
以小麦千粒重为40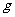 计算,则麦粒总质量达7000亿吨--国王是拿不出来的。
计算,则麦粒总质量达7000亿吨--国王是拿不出来的。
例1.6本不同的书,按下列要求各有多少种不同的选法:
⑴ 分给甲、乙、丙三人,每人两本;
⑵ 分为三份,每份两本;
⑶ 分为三份,一份一本,一份两本,一份三本;
⑷ 分给甲、乙、丙三人,一人一本,一人两本,一人三本;
⑸ 分给甲、乙、丙三人,每人至少一本.
解:⑴ 根据分步计数原理得到: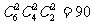 种.
种.
⑵ 分给甲、乙、丙三人,每人两本有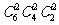 种方法,这个过程可以分两步完成:第一步分为三份,每份两本,设有x种方法;第二步再将这三份分给甲、乙、丙三名同学有
种方法,这个过程可以分两步完成:第一步分为三份,每份两本,设有x种方法;第二步再将这三份分给甲、乙、丙三名同学有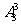 种方法.根据分步计数原理可得:
种方法.根据分步计数原理可得: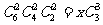 ,所以
,所以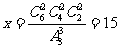 .因此分为三份,每份两本一共有15种方法.
.因此分为三份,每份两本一共有15种方法.
注:本题是分组中的“均匀分组”问题.
⑶ 这是“不均匀分组”问题,一共有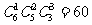 种方法.
种方法.
⑷ 在⑶的基础上在进行全排列,所以一共有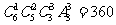 种方法.
种方法.
⑸ 可以分为三类情况:①“2、2、2型”即⑴中的分配情况,有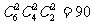 种方法;②“1、2、3型”即⑷中的分配情况,有
种方法;②“1、2、3型”即⑷中的分配情况,有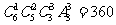 种方法;③“1、1、4型”,有
种方法;③“1、1、4型”,有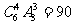 种方法.所以一共有90+360+90=540种方法.
种方法.所以一共有90+360+90=540种方法.
例2.身高互不相同的7名运动员站成一排,甲、乙、丙三人自左向右从高到矮排列且互不相邻的排法有多少种?
解:(插空法)现将其余4个同学进行全排列一共有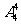 种方法,再将甲、乙、丙三名同学插入5个空位置中(但无需要进行排列)有
种方法,再将甲、乙、丙三名同学插入5个空位置中(但无需要进行排列)有 种方法.根据分步计数原理,一共有
种方法.根据分步计数原理,一共有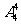
 =240种方法.
=240种方法.
例3.⑴ 四个不同的小球放入四个不同的盒中,一共有多少种不同的放法?
⑵ 四个不同的小球放入四个不同的盒中且恰有一个空盒的放法有多少种?
解:⑴ 根据分步计数原理:一共有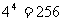 种方法.
种方法.
⑵(捆绑法)第一步从四个不同的小球中任取两个“捆绑”在一起看成一个元素有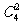 种方法,第二步从四个不同的盒取其中的三个将球放入有
种方法,第二步从四个不同的盒取其中的三个将球放入有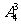 种方法.所以一共有
种方法.所以一共有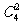
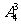 =144种方法.
=144种方法.
例4.马路上有编号为1,2,3,…,10的十盏路灯,为节约用电又不影响照明,可以把其中3盏灯关掉,但不可以同时关掉相邻的两盏或三盏,在两端的灯都不能关掉的情况下,有多少种不同的关灯方法?
解:(插空法)本题等价于在7只亮着的路灯之间的6个空档中插入3只熄掉的灯,故所求方法总数为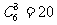 种方法.
种方法.
例5.九张卡片分别写着数字0,1,2,…,8,从中取出三张排成一排组成一个三位数,如果6可以当作9使用,问可以组成多少个三位数?
解:可以分为两类情况:①
若取出6,则有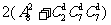 种方法;②若不取6,则有
种方法;②若不取6,则有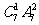 种方法.根据分类计数原理,一共有
种方法.根据分类计数原理,一共有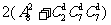 +
+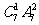 =602种方法.
=602种方法.
2.排列和组合的有关概念及相关性质.
1.两个基本原理;
17、锌是人体生长发育、维持器官正常功能的微量元素,人体缺锌会引起多种疾病,因此缺锌者可通过服用葡萄糖酸锌等保健品来补锌。已知葡萄糖锌的化学式为C12H22O14Zn(相对分子质量为455)。请回答:
(1)葡萄糖酸锌是由___________种元素组成的。
(2)葡萄糖酸锌中所含锌元素的质量分数为__________(结果保留至0.1%)。
(3)现有一支20mL的葡萄糖酸锌口服液,其中含锌6.5mg,那么该口服液中葡萄糖酸锌的质量是_________ mg。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com