7．A．解析：由正弦定理得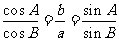，所以sinA·cosA=sinB·cosB，所以sin2A=sin2B，所以2A=2B或2A+2B=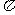，但a≠b，所以2A≠2B，A+B=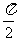，即△ABC是直角三角形．

6．D．解析：该几何体是三棱锥，所以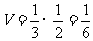，选D．

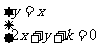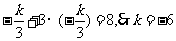5．B．解析：由图(略)，联立方程得，代入，选B．

4．A．解析：P=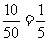，选A．

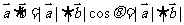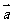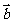3．D．解析：，∴cos=1，=0，所以∥．但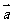∥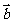时可能它们方向相反，选D．

2．C．解析：a₃=a₁·q²，所以q²=2，q=±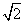，a₄=a₁·q³=±2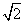，选C．

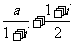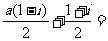
1．B．解析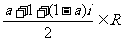：∵=，∴，选B．

21．(本题满分14分)已知数列{a_n}满足a₁=5，a₂=5，a_n+1=a_n+6a_n－1(n≥2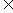，nN^*)．

(1)求证：当n≥2时，{a_n+2a_n－1}和{a_n－3a_n－1}均为等比数列；

(2)求证：当k为奇数时，；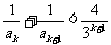

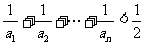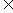(3)求证：(nN^*)．

[答案及详细解析]

20．(本题满分14分)已知函数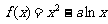在是增函数,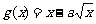在(0,1)为减函数.

(1)求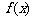、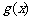的表达式；

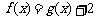(2)求证:当时,方程有唯一解．

19．(本题满分14分)设圆M：x²+y²=8，将圆上每一点的横坐标不变，纵坐标压缩到原来的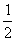，得到曲线C．点M(2，1)，平行于OM的直线l在y轴上的截距为m(m≠0)，l交曲线C于A、B两个不同点．

(1)求曲线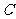的方程；

(2)求m的取值范围．