
1.(08龙岩)函数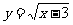 的自变量x的取值范围是
.
的自变量x的取值范围是
.
21.解:(1)由an+1=an+6an-1(n≥2,n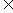 N*)得:
N*)得:
an+1+2an=3(an+2an-1),an+1-3an= -2(an-3an-1) …………………… 2分
且a2+2a1=15,a2-3a1=-10.
∴当n≥2时,{an+2an-1}是首项为15公比为3的等比数列,
{an-3an-1}是首项为-10,公比为-2的等比数列. …………………… 4分
(2)由(1)得an+1+2an=15×3n-1,an+1-3an=-10×(-2)n-
以上两式相减得an=3n-(-2)n . …………………… 8分
当k为奇数时,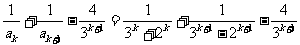
=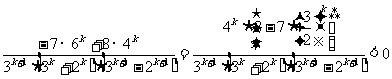 ,
,
∴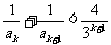 .
…………………… 11分
.
…………………… 11分
(3)由(2)知,当k为奇数时,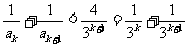 ;
;
∴当n为偶数时,
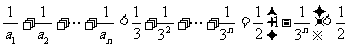 ;
;
当n为奇数时,
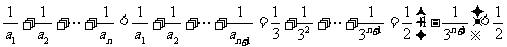 .
.
…………………… 14分
20.解: (I)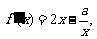 依题意
依题意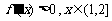 ,即
,即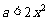 ,
,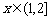 .
.
∵上式恒成立,∴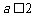 . ① ………………………2分
. ① ………………………2分
又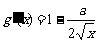 ,依题意
,依题意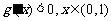 ,即
,即 ,
,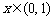 .
.
∵上式恒成立,∴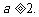 ②
……………………4分
②
……………………4分
由①②得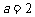 .
……………………5分
.
……………………5分
∴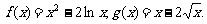 ……………………6分
……………………6分
(II)由(I)可知,方程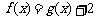 ,
,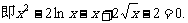
设 ,
,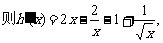 ………………8分
………………8分
令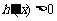 ,并由
,并由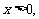 得
得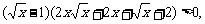 解知
解知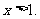 ………………9分
………………9分
令 由
由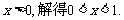 ………………………10分
………………………10分
列表分析:
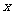 |
(0,1) |
1 |
(1,+¥) |
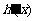 |
- |
0 |
+ |
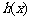 |
递减 |
0 |
递增 |
知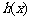 在
在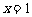 处有一个最小值0,
……………………12分
处有一个最小值0,
……………………12分
当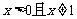 时,
时,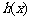 >0,
>0,
∴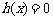 在(0,+¥)上只有一个解.
在(0,+¥)上只有一个解.
即当x>0时,方程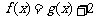 有唯一解.
……………………14分
有唯一解.
……………………14分
19.解:(1)在曲线C上任取一个动点P(x,y),则点(x,2y)在圆x2+y2=8上.
所以有x2+(2y)2=8,即曲线C的方程为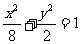 . ………………… 5分
. ………………… 5分
(2)∵直线l平行于OM,且在y轴上的截距为m,又kOM=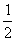 ,
,
∴直线l的方程为y=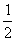 x+m. …………………… 6分
x+m. …………………… 6分
由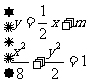 得x2+2mx+2m2-4=0 . ……………………
9分
得x2+2mx+2m2-4=0 . ……………………
9分
又∵直线l交曲线C于A、B两个不同点,
∴△=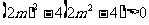 ,解得-2<m<2, ……………………
12分
,解得-2<m<2, ……………………
12分
又∵m≠0,∴m的取值范围是-2<m<0或0<m<2. …………………… 14分
18.解:(1)∵点A、D分别是RB、RC的中点,
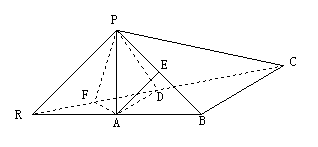 ∴AD∥
∴AD∥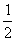 BC.
……………1分
BC.
……………1分
∴∠PAD=∠RAD=∠RBC=90º,
∴PA⊥AD,
∴PA⊥BC . ……………2分
又∵PA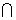 AB=A,BC⊥BA,
AB=A,BC⊥BA,
∴BC⊥平面PAB, ……………3分
∴BC⊥PB. ……………4分
(2)取线段PB的中点E,连结AE,PR. ……………5分
显然,平面PAB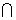 平面PCD=PR.
平面PCD=PR.
∵RA=BA,BE=PE,
∴AE∥PR. ……………6分
又∵AE 平面PRC,
平面PRC,
∴AE∥平面PRC(即平面PDC), ……………7分
故线段PB的中点E是符合题意要求的点. ……………8分
(3)法一:取RD的中点F,连结AF、PF. ……………9分
∵RA=AD=1,AP⊥AR且AP⊥AD,AP=1,
∴PR=PD=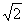 ,
,
∴AF⊥DR,PF⊥DR,
∴∠AFP是二面角A-CD-P的平面角 . ……………11分
∵DR=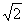 ,∴AF=
,∴AF=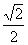 ,PF=
,PF=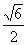 ∴cos∠AFP=
∴cos∠AFP=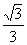 ……………13分
……………13分
法二:建立如图所示的空间直角坐标系A-xyz,
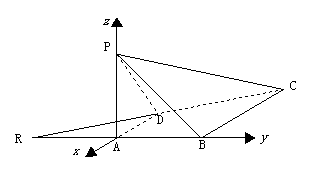 则D(-1,0,0),C(-2,1,0),P(0,0,1)
则D(-1,0,0),C(-2,1,0),P(0,0,1)
∴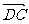 =(-1,1,0),
=(-1,1,0),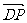 =(1,0,1).
=(1,0,1).
设平面PCD的法向量为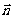 =(x,y,z),则
=(x,y,z),则
 ,
,
令x=1,得y=1,z=-1,
∴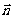 =(1,1,-1).
=(1,1,-1).
显然,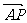 是平面ACD的法向量,
是平面ACD的法向量,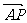 =(0,0,1).
=(0,0,1).
∴cos<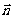 ,
,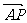 >=
>=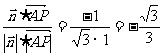 .
.
∴二面角A-CD-P的余弦值为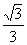 .
……………13分
.
……………13分
17.解:(1)设“这箱产品被用户拒绝接收”为事件A,被接收为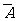 , ………………1分
, ………………1分
则由对立事件概率公式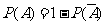 得:
得:
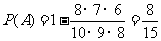 ,
………………5分
,
………………5分
即这箱产品被用户拒绝接收的概率为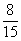 . …………………6分
. …………………6分
(2)x的可能取值为1,2,3. …………………7分
P(x=1)=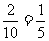 ,
…………………8分
,
…………………8分
P(x=2)=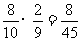 ,
…………………9分
,
…………………9分
P(x=3)=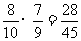 ,
…………………10分
,
…………………10分
x的概率分布列为:
|
x |
1 |
2 |
3 |
…………………11分 |
|
P |
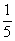 |
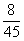 |
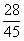 |
数学期望Ex=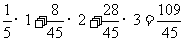 .
…………………13分
.
…………………13分
16.解:(1)∵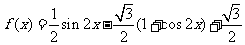 …………2分
…………2分
∴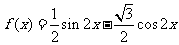
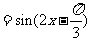 .
…………4分
.
…………4分
∴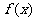 的最小正周期
的最小正周期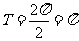 .
…………5分
.
…………5分
又∵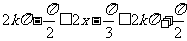 ,
,
∴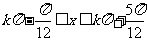 ,
,
所以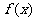 的单调增区间为
的单调增区间为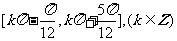 .
…………8分
.
…………8分
(2)令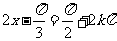 ,则
,则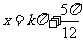
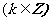 ,
…………10分
,
…………10分
∵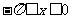 ,
,
∴当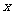 =
=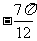 时,
时,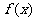 有最大值1. …………12分
有最大值1. …………12分
(二)选做题(13-15题,考生只能从中选做两题)
13.1.解析: :
: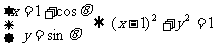 ;则圆心坐标为
;则圆心坐标为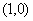 .
.
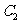 :
: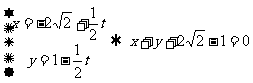 由点到直线的距离公式得圆心到直线的距离为
由点到直线的距离公式得圆心到直线的距离为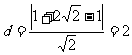 ,所以要求的最短距离为
,所以要求的最短距离为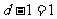 .
.
14.[-1,3] .对任意实数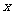 ,关于
,关于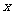 的不等式
的不等式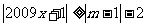 恒成立,则
恒成立,则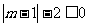 ,解之得
,解之得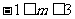 ,故实数
,故实数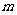 的取值范围是[-1,3] .
的取值范围是[-1,3] .
15.连结AC、BC,则∠ACD=∠ABC,又因为∠ADC=∠ACB=90º,所以△ACD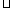 △ACB,所以
△ACB,所以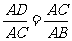 ,解得AC=
,解得AC=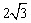 .
.
(一)必做题(9-12题)
9.-10.解析:Tr+1= ,令5-2r=3得r=1,所以x3的系数为(-2)1·
,令5-2r=3得r=1,所以x3的系数为(-2)1·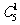 =-10.
=-10.
10.13.解析:S=[log21]+ [log22]+ [log23]+ [log24]+ [log25]+ [log26]+ [log27]+ [log28] =0+1+1+2+2+2+2+3=13.
11.相交.解析:因为点M在圆C外,所以x02+y02>r2,又因为圆心C(0,0)到l的距离d=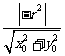 <r,所以l与圆C相交.
<r,所以l与圆C相交.
12.17,2×3n-1-1.解析:第3个图形中有1+4+3×4=17个三角形,第n个图形中有1+4+3×4+32×4+……+3n-2×4=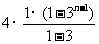 =1+2×(3n-1-1)=2×3n-1-1个三角形.
=1+2×(3n-1-1)=2×3n-1-1个三角形.
8.C.解析:f(x)+5≤f(x+5)≤f(x+4)+1<……<f(x+1)+4≤f(x)+5,所以f(x)+5≤f(x+1)+4≤f(x)+5,即f(x)+1≤f(x+1)≤f(x)+1,即f(x+1)=f(x)+1,所以g(2009)=f(2009)+1-2009=f(1)+2008+1-2009=1,选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com