
3. 设正方体的棱长为,则它的外接球的表面积为 ( )
A.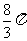 B.2π C.4π D.
B.2π C.4π D.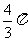
2.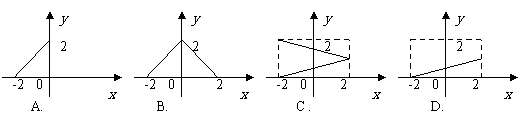 集合
集合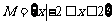 ,
,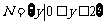 ,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是
( ).
,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是
( ).
1.下列函数中,在其定义域内既是奇函数又是减函数是的 ( )
A. B.
B.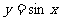
C.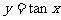 D.
D.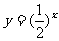
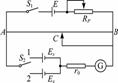 [例11]如图31所示的电路可测电源电动势,图中E为供电电源,Es为标准电源,Ex为待测电源,RP是限流电阻,r0是电流表G的保护电阻.测量时,首先闭合开关S1,电阻丝AB上有一定的电势降落;接着将开关S2合到“1”位置,滑动触法C使G指针指零,此时AC长度为L1;再将S2合到“2”位置,滑动触头C使G指针再指零,此时AC长度为L2.
[例11]如图31所示的电路可测电源电动势,图中E为供电电源,Es为标准电源,Ex为待测电源,RP是限流电阻,r0是电流表G的保护电阻.测量时,首先闭合开关S1,电阻丝AB上有一定的电势降落;接着将开关S2合到“1”位置,滑动触法C使G指针指零,此时AC长度为L1;再将S2合到“2”位置,滑动触头C使G指针再指零,此时AC长度为L2.
①若仅闭合S1时流过AB的电流为I0,那么当S2分别合到“1”、“2”上后,通过滑动触头C使G指针指零时,流过AC段的电流分别是_____和_____. 图31
②由题中的已知量求得待测电源的电动势Ex=_____.
[解析]由题意知,开关S2接1,滑动触头C使电流计读数为零,则此时AC段电压降必为ES(电桥平衡);同理,当S2接2,滑动触头C使电流计读数为零时,此时AC段电压降必为Ex.两次流过AB的干路电流不变,则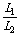 =
=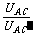 =
=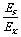 ,故Ex=
,故Ex=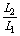 Es.
Es.
[例12]现有一待测电源,其内阻未知,另有电流表A1和A2,伏特表V1和V2,四电表都是非理想电表,但内阻未知.还有开关和导线及一只灵敏电流G,请设计电路图,测出电源电动势E和内阻r.
[解析]本题因提供了灵敏电流表G,故考虑用电桥平衡法则电源电动势和内阻,电路图如图34所示.闭合开关S,通过调节滑动变阻器R1、R2,可以使电流计G的示数为0,则此时电流表A1和A2读数之和就是流过电源的电流(即干路电流),电压表V1、V2读数之和就是电源的路端电压.再次调节R1、R2,使电流计的读数再变为0,再读出四个电表的读数.根据两测量读数列出方程,便可求出电源的电动势和内电阻,并且不必考虑电表带来的误差.因为此时四个电表相当于电源的外电路电阻.
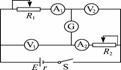 假设第一次两电流表之积为I1,两电压表读数之和为U1,则E=U1+I1r,第二次两电流表
假设第一次两电流表之积为I1,两电压表读数之和为U1,则E=U1+I1r,第二次两电流表
读数之和为I2,两电压表读数之和为U2,则有E=U2+I2r 图32
解两方程有:E= , r=
, r=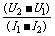
[点评]在实际测量时,只要选择适当的电表,注意到它们的精确度,量程以及读数上的匹配,来确保读出数值的精确性,就可以使电动势和内阻的测量达到满意的效果.本方法设有因为电表有内阻而产生系统误差,是一种极为巧妙的方法.让我们再一次为创新思维的美喝彩!
如图27所示电路图中,多次改变电阻箱的阻值,记下电阻箱的阻值R及相应的电压表的读数U.设电源电动势为E,电压表的内阻为Rv,由分压原理有
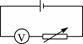
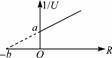
图27 图28
U=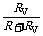 E,化得
E,化得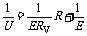 ,作出
,作出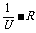 图象如图28所示,为一条直线.其截距a=1/E,斜率为
图象如图28所示,为一条直线.其截距a=1/E,斜率为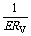 =
=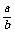 ,则RV=b.这是一种测电源电动势和电压表内阻的巧妙办法.
,则RV=b.这是一种测电源电动势和电压表内阻的巧妙办法.
[例10]在做测量电源的电动势E和内阻r的实验时,提供的器材有:待测电源一个,已知内阻为RA的电流表一个,电阻箱一个,开关一个,导线若干.
为使测量更加准确,多次改变电阻箱的阻值R,读出电流表的相应示数I,以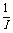 为纵坐标,R为横坐标,画出
为纵坐标,R为横坐标,画出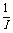 与R的关系图线是一条直线,如图(b)所示.图线延长可得直线在纵轴的截距为m,直线的斜率为k.
与R的关系图线是一条直线,如图(b)所示.图线延长可得直线在纵轴的截距为m,直线的斜率为k.
(1)E=_________,r=_________.
(2)在虚线框图29(a)中画出实验电路图.
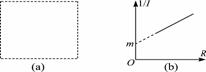
图29
[解析]本题明确电流表内阻为RA,说明RA不能忽略.虽然处理数据方法从U-I图线改变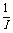 -R图线,但“
-R图线,但“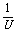 -R法”的原理没有变.
-R法”的原理没有变.
 (1)E=
(1)E=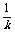 ,r=
,r=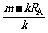
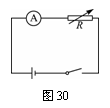
(2)如图30(RA不能忽略,根据全电路欧姆定律,I=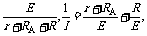 可知
可知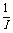 -R图线为直线,其斜率k=
-R图线为直线,其斜率k=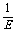 ,截距m=
,截距m=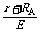 .则E=
.则E=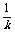 ,r=
,r=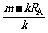 )
)
如图25所示,两只电压表V1和V2,其量程已知,V1的内阻RV1已知,V2内阻不知为多少,电源内能不可忽略,且未知,电源电动势不超过电压表的量程.先合上开关S,记下V1的示数U1;再断开开关S,记下V1和V2的示数U1′和U2′,有
E=U1+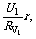 E=U2′+U1′+
E=U2′+U1′+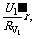
联立方式有 E=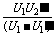 ,r=
,r=
[例9]如图26所示电路中,当电键S断开时,电压表V1的示数为12V,电压表V2的示数为6V.当电键S闭合时,电压表V2的示数为15V,求电源的电动势.
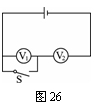 [解析]设电压表V1的内阻为R1,电压表V2的内阻为R2,则有
[解析]设电压表V1的内阻为R1,电压表V2的内阻为R2,则有
电键S断开时:U1+U2=E-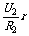
电键S闭合时:U2′=E-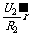
代入数据有12+6=E-6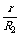 ,15=E-15
,15=E-15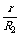
将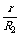 当成一个未知数,则可解得E=20V.
当成一个未知数,则可解得E=20V.
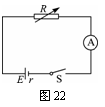 如图22所示电路图,测出总电流及外电阻,由全电路的欧姆定律知有
如图22所示电路图,测出总电流及外电阻,由全电路的欧姆定律知有
E=I1(R1+r), E=I2(R2+r) 则
E=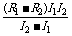 ,
,
r=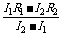 .
.
显然,理论上只需两组I,R值即可,但实际这样的误差太大,应多测几组已便求平均值.也可由U=IR把变量R转换成U,再对U-I图线进行数据的处理.由于电流表内阻RA的分压作用,经分析可知电动势的测量值与真实值相等,即E测=E真,而内值偏大,即r测=RA+r真.本实验的基本器材为电流表和电阻箱.
[例8]现有器材:量程为10.0mA,内阻约为30~40W的电流表一个,定值电阻R1=150,定值电阻R2=100,单刀双掷开关S,导线若干.要求利用这些器材测量一干电池(电动势约1.5V)的电动势.
(1)按要求连接实物图(下图23).
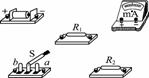
图23
[解析]利用一只电流表和两只定值电阻来测量干电池的电动势,基本的原理是改变外电路的电阻,得到两组电流值.根据闭合电路欧姆定律,得到一个关于电源电动势和内阻的二元一次方程组,解方程组即可求得电动势.由给定的条件知,电流表量程为10mA,内阻圴为30 W ~40 W,电源电动势约1.5V,内阻约几欧,则外电阻的选择条件为
10×10-3≥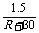 ,即R≥
,即R≥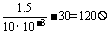 ,
,
故外电阻可选R1或(R1+R2).
(1)连接实物图如下图24所示.

图24
(2)当单刀双掷开关掷向b时,R1为外电阻,得到
I1=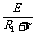 ①
①
当单刀双掷开关掷向a时,R1和R2串联起来作为外电阻时,得到
I2=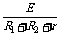 ②
②
式中E、r分别表示干电池的电动势和内阻
联立①②可解得 E=
I1是外电阻为R1时的电流,I2是外电阻为R1和R2串联时的电流.
[点评]本题是利用电阻R1和R2与R2串联分别接入电路,获得两组实验数据,求出E和r.需要注意的是,干电池电压为1.5V,内阻r约为几欧姆,如果用定值电阻R2=100W作为外电阻有10mA<I=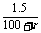 <15mA,则超过了电流表的量程10mA,因此该电阻不能单独使用.
<15mA,则超过了电流表的量程10mA,因此该电阻不能单独使用.
如图17所示,改变电阻箱R的阻值,多测几组路端电压及对应的外电阻阻值.
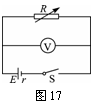 则有U1=E-
则有U1=E-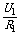 r, U2=E-
r, U2=E-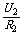 r,结合两式解得
r,结合两式解得
E=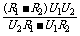 ,
,
r=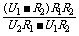
显然,实验时电阻箱接入电路的初始值应足够大,再由大到小逐渐调节,可多测几组数据,最后求E,r的平均值.也可以由I=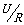 把变量R转换成I,通过U-I图象求E和r.本方法的基本器材为电压表和电阻箱.由于实验中电压表内阻RV的存在,具有分流作用,故测量值均小于真实值.其关系为:
把变量R转换成I,通过U-I图象求E和r.本方法的基本器材为电压表和电阻箱.由于实验中电压表内阻RV的存在,具有分流作用,故测量值均小于真实值.其关系为:
E测=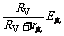 ,r测=
,r测=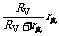 .
.
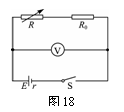 [例6]一种供实验使用的小型电池标称电压为9V,电池允许最大输出电流为50 mA,为了测定这个电池的电动势和内阻,用图18所示电路进行测量(图中电压表内阻很大,可不考虑它对测量的影响),R为电阻箱,阻值范围为0~9999,R0是保护电阻.
[例6]一种供实验使用的小型电池标称电压为9V,电池允许最大输出电流为50 mA,为了测定这个电池的电动势和内阻,用图18所示电路进行测量(图中电压表内阻很大,可不考虑它对测量的影响),R为电阻箱,阻值范围为0~9999,R0是保护电阻.
(1)实验室里备用的定值电阻有以下几种规格:
A.10,5W
B.150,0.5W
C.200 ,0.25W
D.1.2 k ,1W
实验时,R0应选用______较好.
(2)在实验中当电阻箱调到图19所示位置后,闭合开关S,电压表示数9.0V,变阻箱此时电阻为____,电路中流过电阻箱的电流为____mA.
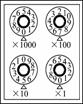

图19 图20
(3)断开开关,调整电阻箱阻值,再闭合开关,读取电压表示数,多次测量后,做出如上图20所示图线,则该电池电动势E=_____V,内阻r=__ __ .
[解析](1)保护电阻R0的选择关系到能否控制电源的输出电流在50mA以下,取电阻箱电阻
R=0,则R0+r=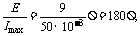
实验室里备用的定值电阻150 W(B)和200 W(C)均接近180 W,比较它们的额定电流,
IB=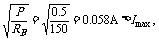
故应选电阻B作为保护电阻,即R0=150 W,选B.
(2)电阻箱的读数为750 W,通过电阻箱的电流为:
I0=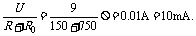
(3)延长U-I图线,与纵轴的交点即电流电动势,E=9.5V,电源内阻
r=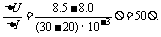
[点评]实际测量电路中往往接有保护电阻,选择保护电阻,不仅要看电阻的大小,还要看允许通过的电流.本题采用U-R法的测量电路测量电源电动势和内阻,在处理数据时采用U-I法的处理方法.U-I图线上各坐标点的电流值是由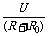 得到的.
得到的.
[例7](上海高考题)现有一阻值为10 W的定值电阻、一只开关、导线若干及一只电压表,该电压表表面上有刻度但无刻度值.要求设计一个能测定某电源内阻的实验方案(已知电压表内阻很大,电压表量程大于电源电动势,电源内阻约为几欧).要求:
(1)画出实验电路图.
(2)简要写出完成接线后的实验步骤.
(3)写出用测得的量计算电源内阻的表达式r=_____.
[解析](1) 实验电路如图21所示.
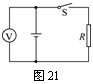 (2)实验步骤如下:
(2)实验步骤如下:
①断开开关,记下电压表偏转格数N1;
②合上开关,记下电压表偏转格数N2;
③电源内阻按下列公式计算:
r=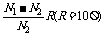
(3)由于电压表内阻很大,因此当断开开关S时测得的路端电压U1等于电源电动势.
设电压表每格的电压值为U0,则有
E=U1=N1U0 ①
同样,由于电压表的内阻很大,在合上开关S后,外电路的总电阻可以认为等于R=10W,因此有
E=U2+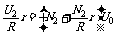 ②
②
联立①、②两式得 r=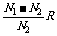
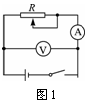 这是课本上提供的常规方法,基本原理是利用全电路欧姆定律,即U =E-Ir,测出路端电压及电路中的总电流,用解方程组的办法求出电动势和内阻.原理图如图1所示,实验基本器材为电压表和电流表.改变不同的R值,即可测出两组不同的U和I的数据,有
这是课本上提供的常规方法,基本原理是利用全电路欧姆定律,即U =E-Ir,测出路端电压及电路中的总电流,用解方程组的办法求出电动势和内阻.原理图如图1所示,实验基本器材为电压表和电流表.改变不同的R值,即可测出两组不同的U和I的数据,有
E =U1+I1r ①,E =U2+I2r ②
由①②式得:
E =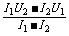 ,r =
,r =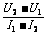 .
.
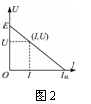 多测几组U、I数据,分别求出每组测量数据对应的E,r值,最后求出平均值.还可以用图象确定电池的电动势和内电阻.由U=E-Ir知,对于确定的电池,E,r为定值,U是I的一次函数,U与I的对应关系图象是一条直线.其图象持点有:
多测几组U、I数据,分别求出每组测量数据对应的E,r值,最后求出平均值.还可以用图象确定电池的电动势和内电阻.由U=E-Ir知,对于确定的电池,E,r为定值,U是I的一次函数,U与I的对应关系图象是一条直线.其图象持点有:
①当I=0时,U=E,这就是说,当外电路断路时,路端电压等于电源电动势.所以反映在U-I图线上是图线在纵轴U上的截距(等于电源的电动势E).如图2.
②当R=0时,U=0,这时I=I短=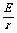 .即是,当电源短路时,路端电压为零.这时电路中的电流并不是无穷大,而是等于短路电路I短.反映在U-I图线上是图线在横轴I上的截距(等于I短),如图2所示.根据I短=
.即是,当电源短路时,路端电压为零.这时电路中的电流并不是无穷大,而是等于短路电路I短.反映在U-I图线上是图线在横轴I上的截距(等于I短),如图2所示.根据I短=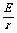 ,可知r =
,可知r =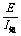 .这样,从图中求出E和I短,就能计算出r.
.这样,从图中求出E和I短,就能计算出r.
对于r =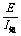 ,对比图线可以看出,
,对比图线可以看出,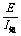 实际上就是U-I图线斜率的大小(斜率取绝对值).所以求电源内阻r变成了求图线斜率的大小.
实际上就是U-I图线斜率的大小(斜率取绝对值).所以求电源内阻r变成了求图线斜率的大小.
 由于实际实验中数据采集范围的限制以及作图的规范,使得这个实验的U-I图线的纵轴起点一般并不是零,因为若不这样取法将会使全图的下半部变为空白,图线只集中在图的上面的
由于实际实验中数据采集范围的限制以及作图的规范,使得这个实验的U-I图线的纵轴起点一般并不是零,因为若不这样取法将会使全图的下半部变为空白,图线只集中在图的上面的 部分,它既不符合作图要求,又难找出图线与横轴的关系.一般说来纵轴的起点要视电压的实验值(最小值)而定,但图线与横轴的交点不再是短路电流了.常在这里设考点,值得引起注意.
部分,它既不符合作图要求,又难找出图线与横轴的关系.一般说来纵轴的起点要视电压的实验值(最小值)而定,但图线与横轴的交点不再是短路电流了.常在这里设考点,值得引起注意.
这样一来就不能从图线上得到短路电流I短.在这种情况下一般是从图线上任取两点A、B,利用A、B两点的数值求得图线的斜率以获得电源电阻r的值.如图3所示.r的数值应是
r=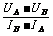
当然,也可以是 r=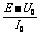
其中U0是纵轴的起点值,I0是此时横轴的截距.注意,这里的I0并不是短路电流I短.
[例1]在做测量干电池的电动势和内电阻的实验时,备有下列器材供选用:
A.干电池一节(电动势约1.5V)
B.直流电流表(量程0~0.6~3A,0.6A挡内阻0.10 ,3A挡内阻0.025)
C.直流电压表(量程0~3~15V,3V挡内阻5k,15V挡内阻25k)
D.滑动变阻器(阻值范围0~15,允许最大电流1A)
E.滑动变阻器(阻值范围0~1000,允许最大电流0.5A)
F.开关 G.导线若干根 H.电池夹
(1)将按本实验要求选定的器材(系统误差较小),在下图4所示的实物图上连线.
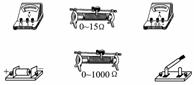
图4
(2)如图5所示,电流表指针停止在下图(1)所示位置,量程取0.6A挡时读数为______;量程取3A挡时读数为_______.电压表指针停在图(2)所示位置,量程取3V挡时读数为______;取量程为15V挡时读数为______.
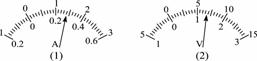
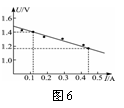 图5
图5
(3)根据实验记录,画出的U-I图象如图6所示,可得待测电池的内电阻r为_______W.
[解析]本例是典型的U-I法测电源电动势和内电阻,且运用图象处理数据.
(1)连接图如图7所示.
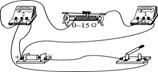 图7
图7
由于电路中的电压为1.5V,电路中的电流不超过0.6A,因此,电压表应选0~3V量程,电流表应选择0~0.6A量程.为了使电流值可调范围大一些,滑动变阻器应选择0~15W,为了减小误差,采用电流表内接法.
(2)电流表读数在0.6A挡时,I=0.280A,在3A挡时,I=1.40A,电压表读数在3V挡时,U=1.30V,在15V挡时,U=6.50V.
|
组别 |
I(A) |
U(V) |
|
1 |
0.12 |
1.37 |
|
2 |
0.20 |
1.32 |
|
3 |
0.31 |
1.24 |
|
4 |
0.32 |
1.18 |
|
5 |
0.50 |
1.10 |
|
6 |
0.57 |
1.05 |
(3)r= =
=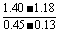 W=0.69W.
W=0.69W.
[点评]本例采用的是电流表内接的U-I法,但有系统误差,如图8所示,这是由于电压表的分流IV,使电流表示值I小于电池的输出电流I真,I真=I+IV,而IV =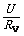 ,显见U越大IV越大,只有短路时U =0才有I真=I=I短,即B点,它们的关系可用图9表示,实测的图线为AB,经过IV修正后的图线为A′B,即实测的r和E都小于真实值.实验室中J0408型电压表0~3V挡内阻为3kW,实验中变阻器R的取值一般不超过30W,所以电压表的分流影响不大,利用欧姆定律可导出r=
,显见U越大IV越大,只有短路时U =0才有I真=I=I短,即B点,它们的关系可用图9表示,实测的图线为AB,经过IV修正后的图线为A′B,即实测的r和E都小于真实值.实验室中J0408型电压表0~3V挡内阻为3kW,实验中变阻器R的取值一般不超过30W,所以电压表的分流影响不大,利用欧姆定律可导出r=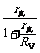 ,E=
,E=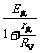 ,可知r<r真,E<E真,为减小系统误差,图8电路要求RV>>r真,这在中学实验室中是容易达到的,所以课本上采取这种电路图.这种接法引起误差的原因都是由于电压表的分流影响.
,可知r<r真,E<E真,为减小系统误差,图8电路要求RV>>r真,这在中学实验室中是容易达到的,所以课本上采取这种电路图.这种接法引起误差的原因都是由于电压表的分流影响.
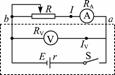

图8 图9
另一种电路是将电流表外接,如图10所示,其等效电路图如图11所示.
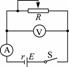
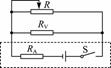
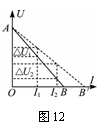 图10
图11
图10
图11
由于电流表的分压UA的影响,使电压表的测量值小于电池的端电压U端=U真,而有U真=U测+UA的关系.且UA=IRA,故电流I越大,UA也越大,当电路断开时,U测=U真,即图12中的A点.实测的图线为AB,当将电流表内阻看成内电路的一部分时(如图11所示),r测=r真+RA,这样处理后,图线可修正为AB′但此时图线与横轴的交点并不为电池的短路电流,由图线可知:E测=E真,r测>r真.只有当RA<<r真时,才有r测=r真.然而中学的实验设备很难达到这一点,故此法不可取.
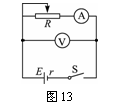 [例2]用电流表和电压表测定电池的电动势E和内电阻r,所用的电路如下图13所示.一位同学测得的数据组如下表中所示.
[例2]用电流表和电压表测定电池的电动势E和内电阻r,所用的电路如下图13所示.一位同学测得的数据组如下表中所示.
(1)试根据这些数据在图中作出U-I图象.
(2)根据图象得出电池的电动势E=______V,电池的内电阻r=______W.
(3)若不作出图象,只选用其中两组U和I数据,可利用公式E=U1+I1r和E=U2+I2r算出E和r,这样做可能得出误差很大的结果,选用第_____组和第_____组的数据,求得的E和r误差最大.
[解析]如图14所示,作图象时应把个别不合理的数据排除.由直线与纵轴的交点可读出电动势E=1.45V,再读出直线与横轴的交点的坐标(U,I ),连同得出的E值代入E=U+Ir中,得r=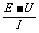 =
= =0.69W.
=0.69W.
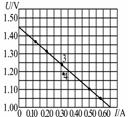
图14
选用第3组和第4组数据求得的E和r误差最大,不需要利用所给的6组数据分别进行计算,利用作图就可看出这一点.选用这两组数据求E和r,相当于过图中3和4两点作一直线,利用此直线求出E和r,而此直线与所画直线偏离最大.实际上,第4组数据不合理,已经排除.
[点评]用图象法处理数据是该实验的一个重点,在高考中经常出现.需要注意两点,如果U-I图象的坐标原点是U轴、I轴的零点,那么图象与U轴交点表示电源的电动势E,与I轴交点表示电源短路的电流,内阻r=E/I短,当然,电源内阻也可以用r=DU/DI求得;如果U-I图象的坐标原点是I轴零点,而非U轴零点,那么图象与U轴交点仍表示电源的电动势E,而图象与I轴交点不表示电源短路时的电流,内阻只能用r=DU/DI求解.
[例3]在测定一节干电池的电动势和内电阻的实验中,备有下列器材:
A.干电池(电动势E约1.5V,内电阻r小于1.5W)
B.电流表G(满偏电流3mA,内阻Rg=10W)
C.电流表A(0~0.6A,内阻约为0.1W)
D.滑动变阻器R1(0~20,10A)
E.滑动变阻器R2(0~100,1A)
 F.定值电阻R3=990W
F.定值电阻R3=990W
G.开关,导线若干
(1)为了方便且能较准确地进行测量,其中应选用的滑动变阻器为_______(填数字代号).
(2)请画出利用本题提供的器材所设计的测量电池电动势和内阻的实验电路图.
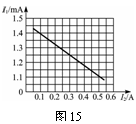
(3)图15为某同学根据正确的电路图作出的I1-I2图线(I1为电流表G的示数,I2为安培表A的示数),由该图线可得被测干电池的电动势E=______,内电阻r=______.
[解析]与典型的U-I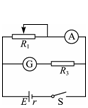 法测电动势及内阻的实验相比,本题所提供的器材中缺少电压表,但多了一块电流表和定值电阻,能否将其中一块电流表先改装成电压表再按U-I法测定呢?进一步定量分析可知,电流表G的满偏电流3mA,内阻Rg=10W,若将其与定值电阻R3=990W串联,就可改装成量程为3V的电压表了,其读数为U=1000I1.由I1-I2图线知:纵坐标I1乘以1000即可转换为U-I2图线,由此可算出E和r.因此不难获得正确答案:
法测电动势及内阻的实验相比,本题所提供的器材中缺少电压表,但多了一块电流表和定值电阻,能否将其中一块电流表先改装成电压表再按U-I法测定呢?进一步定量分析可知,电流表G的满偏电流3mA,内阻Rg=10W,若将其与定值电阻R3=990W串联,就可改装成量程为3V的电压表了,其读数为U=1000I1.由I1-I2图线知:纵坐标I1乘以1000即可转换为U-I2图线,由此可算出E和r.因此不难获得正确答案:
(1)选D;
(2)电路图如图16所示.
(3)E=1.47V,r=0.74W.
[点评]若实验中给定的是双电压表,同样应根据题给条件,以运用电流表和电压表测定电源电动势和内阻的实验方法作为实验设计的起点,确定能否将某个电压表当电流表使用.例如,量程较小的(如mV)电压表,且已知其内阻时,就可以视其为电流表,其电流值为IV=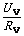 .这样同样可以满足实验要求.
.这样同样可以满足实验要求.
10. 如图,点A坐标为(-1,1),将此小船ABCD向左平移2个单位,再向上平移3个单位得A′B′C′D′.
(1)画出平面直角坐标系;
 (2)画出平移后的小船A′B′C′D′,写出A′,B′,C′,D′各点的坐标.
(2)画出平移后的小船A′B′C′D′,写出A′,B′,C′,D′各点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com