
2.对正整数n,设曲线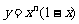 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为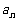 ,则数
,则数
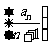 的前n项和的公式是
的前n项和的公式是
1.若曲线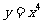 的一条切线
的一条切线 与直线
与直线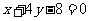 垂直,则
垂直,则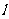 的方程为( )
的方程为( )
A.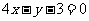 B.
B.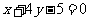 C.
C.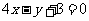 D.
D.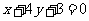
7.[答案](1)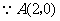 ,
,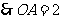 .
.
作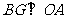 于
于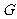 ,
,
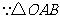 为正三角形,
为正三角形,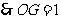 ,
,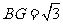 .
.
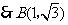 .
.
连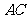 ,
,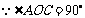 ,
,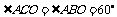 ,
,
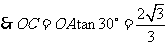 .
.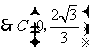 .
.
(2)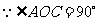 ,
,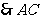 是圆的直径,
是圆的直径,
又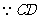 是圆的切线,
是圆的切线,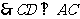 .
.
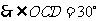 ,
,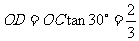 .
.
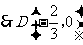 .
.
设直线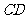 的函数解析式为
的函数解析式为 ,
,
则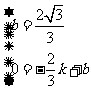 ,解得
,解得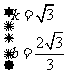 .
.
 直线
直线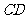 的函数解析式为
的函数解析式为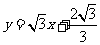 .
.
(3)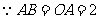 ,
,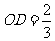 ,
,
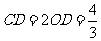 ,
,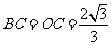 ,
,
 四边形
四边形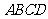 的周长
的周长 .
.
设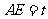 ,
,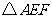 的面积为
的面积为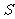 ,
,
则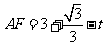 ,
,
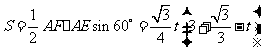 .
.
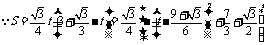 .
.
 当
当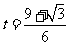 时,
时,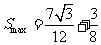 .
.
 点
点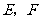 分别在线段
分别在线段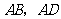 上,
上,
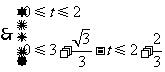 ,
,
解得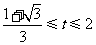 .
.
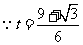 满足
满足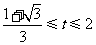 ,
,
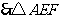 的最大面积为
的最大面积为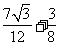 .
.
6.[答案](1)解法一:∵抛物线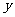 =-
=-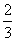

 +
+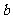
 +
+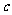 经过点A(0,-4),
经过点A(0,-4),
∴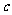 =-4
=-4
又由题意可知,
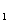 、
、
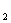 是方程-
是方程-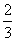

 +
+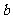
 +
+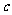 =0的两个根,
=0的两个根,
∴
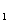 +
+
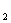 =
=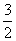
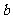 ,
, 
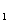

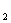 =-
=-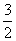
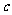 =6
=6
由已知得(
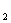 -
-
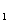 )
) =25
=25
又(
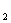 -
-
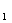 )
) =(
=(
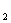 +
+
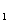 )
) -4
-4
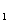

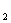 =
=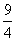
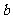
 -24
-24
∴ 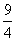
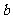
 -24=25 ,解得
-24=25 ,解得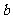 =±
=±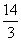
当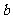 =
=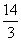 时,抛物线与
时,抛物线与 轴的交点在
轴的交点在 轴的正半轴上,不合题意,舍去.
轴的正半轴上,不合题意,舍去.
∴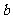 =-
=-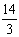 .
.
解法二:∵
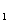 、
、
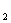 是方程-
是方程-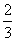

 +
+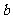
 +c=0的两个根,
+c=0的两个根,
即方程2
 -3
-3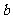
 +12=0的两个根.
+12=0的两个根.
∴ =
=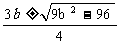 ,
,
∴
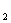 -
-
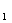 =
=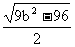 =5,
=5,
解得 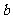 =±
=±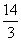 (以下与解法一相同.)
(以下与解法一相同.)
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,
又∵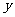 =-
=-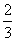

 -
-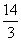
 -4=-
-4=-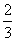 (
( +
+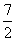 )
) +
+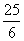
∴抛物线的顶点(-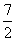 ,
,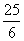 )即为所求的点D.
)即为所求的点D.
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),
根据菱形的性质,点P必是直线 =-3与
=-3与
抛物线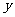 =-
=-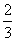

 -
-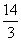
 -4的交点,
-4的交点,
∴当 =-3时,
=-3时,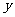 =-
=-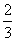 ×(-3)
×(-3) -
-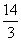 ×(-3)-4=4,
×(-3)-4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形.
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上.
5.[解析]解决问题(1)(2)的关键是利用图中的相似三角形;解决问题(3)时利用(2)中的m、n的关系求出点D的坐标,进而分别求出BD2、CE2、DE2的值;解决问题(4)时,通常方法是先猜想其结论成立,根据结论的特征,尝试构造直角三角形,则问题可轻松获解.
[答案]解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA
∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°
∴∠BAE=∠CDA
又∠B=∠C=45°
∴∆ABE∽∆DCA
(2)∵∆ABE∽∆DCA,∴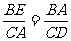
由依题意可知CA=BA=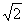
∴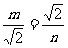 ,∴m=
,∴m=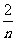
自变量n的取值范围为1<n<2.
(3)由BD=CE可得BE=CD,即m=n
∵m=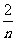 ,∴m=n=
,∴m=n=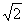
∵OB=OC=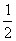 BC=1,∴OE=OD=
BC=1,∴OE=OD=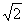 -1,∴D(1-
-1,∴D(1-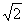 , 0)
, 0)
∴BD=OB-OD=1-(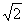 -1)=2-
-1)=2-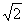 =CE, DE=BC-2BD=2-2(2-
=CE, DE=BC-2BD=2-2(2-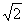 )=2
)=2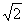 -2
-2
∵BD +CE
+CE =2 BD
=2 BD =2(2-
=2(2-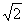 )
) =12-8
=12-8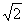 , DE
, DE =(2
=(2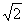 -2)
-2) = 12-8
= 12-8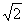
∴BD +CE
+CE =DE
=DE
(4)成立
证明:如图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,则CE=HB,AE=AH,
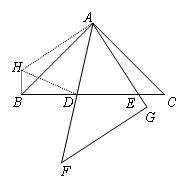
∠ABH=∠C=45°,旋转角∠EAH=90°.
连接HD,在∆EAD和∆HAD中
∵AE=AH, ∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD.
∴∆EAD≌∆HAD
∴DH=DE
又∠HBD=∠ABH+∠ABD=90°
∴BD +HB
+HB =DH
=DH
即BD +CE
+CE =DE
=DE
4.[答案] Ⅰ.证明:∵DEFG为正方形,∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,

求得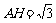 ,由△AGF∽△ABC得:
,由△AGF∽△ABC得: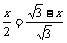
解之得: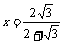 (或
(或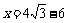 )
)
解法二:设正方形的边长为x,则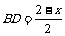
在Rt△BDG中,tan∠B=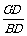 , ∴
, ∴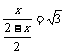
解之得: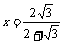 (或
(或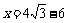 )
)
解法三:设正方形的边长为x,则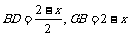
由勾股定理得: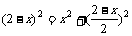 解之得:
解之得: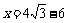
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形 ∵FE∥F’E’ ,
∴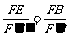 ,同理
,同理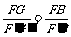 ,∴
,∴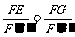
又∵F’E’=F’G’, ∴FE=FG
因此,矩形GDEF为正方形
3.[解析]此题考查圆的切线的判定方法及一次函数解析式的判定,(1)切线的判定要从定义上去判定:过半径的外端,且垂直于半径的直线为圆的切线,所以此题要连接OM,然后证明OM⊥DC,这里平行线对角的转化起到了关键的作用; (2) MC的长借助于勾股定理建立方程而求出,要求直线DC的解析式需要再求出点C的坐标根据MC的长即可以求出点C的坐标(,0),从而求出直线DC的解析式.
[答案](1)答:直线DC与⊙O相切于点M .
证明如下:连OM, ∵DO∥MB,
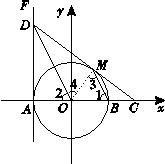
∴∠1=∠2,∠3=∠4 .
∵OB=OM,
∴∠1=∠3 .
∴∠2=∠4 .
在△DAO与△DMO中,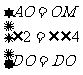
∴△DAO≌△DMO .
∴∠OMD=∠OAD .
由于FA⊥x轴于点A,∴∠OAD=90°.
∴∠OMD=90°. 即OM⊥DC .
∴DC切⊙O于M.
(2)解:由D(-2,4)知OA=2(即⊙O的半径),AD=4 .
由(1)知DM=AD=4,由△OMC∽△DAC,
知= = = ,∴AC=2MC.
在Rt△ACD中,CD=MC+4.
由勾股定理,有(2MC)2+42=(MC+4)2,解得MC= 或MC=0(不合,舍去).
∴MC的长为,∴点C(,0).
设直线DC的解析式为y = kx+b .
则有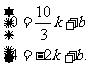 解得
解得
∴直线DC的解析式为 y =-x+.
2.[解析]从表格中的数据我们可以看出当x增加1时,对应y的值减小20,所以y与x之间可能是一次函数的关系,然后设出一次函数关系式,求出其关系式,然后进行验证.
[答案](1)设y与x之间的关系为一次函数,其函数表达式为y=kx+b
将(0,100),(1,80)代入上式得,
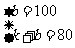 解得
解得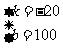
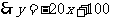
验证:当x=2时,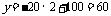 ,符合一次函数;
,符合一次函数;
当x=2.5时,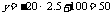 ,也符合一次函数.
,也符合一次函数.
 可用一次函数
可用一次函数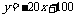 表示其变化规律,
表示其变化规律,
而不用反比例函数、二次函数表示其变化规律.
∴y与x之间的关系是一次函数,其函数表达式为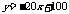
(2)当x=4.2时,由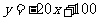 可得y=16
可得y=16
即货车行驶到C处时油箱内余油16升.
(3)方法不唯一,如:
方法一:由(1)得,货车行驶中每小时耗油20升,
设在D处至少加油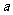 升,货车才能到达B地.
升,货车才能到达B地.
依题意得,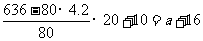 ,
,
解得,a=69(升)
方法二:由(1)得,货车行驶中每小时耗油20升,
汽车行驶18千米的耗油量: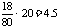 (升)
(升)
D、B之间路程为: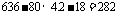 (千米)
(千米)
汽车行驶282千米的耗油量:
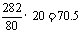 (升)
(升)
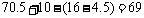 (升)
(升)
方法三:由(1)得,货车行驶中每小时耗油20升,
设在D处加油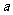 升,货车才能到达B地.
升,货车才能到达B地.
依题意得,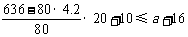 ,
,
解得,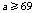
∴在D处至少加油69升,货车才能到达B地.
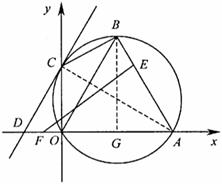
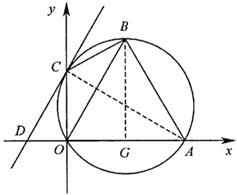
7.(·嘉兴市)如图,直角坐标系中,已知两点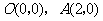 ,点
,点 在第一象限且
在第一象限且 为正三角形,
为正三角形, 的外接圆交
的外接圆交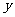 轴的正半轴于点
轴的正半轴于点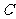 ,过点
,过点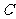 的圆的切线交
的圆的切线交 轴于点
轴于点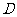 .
.
(1)求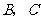 两点的坐标;
两点的坐标;
(2)求直线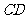 的函数解析式;
的函数解析式;
(3)设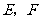 分别是线段
分别是线段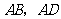 上的两个动点,且
上的两个动点,且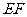 平分四边形
平分四边形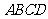 的周长.
的周长.
试探究: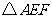 的最大面积?
的最大面积?
第10课时 综合型问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com