
例二:已知无穷数列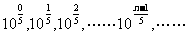 ,
,
求证:(1)这个数列成GP
(2)这个数列中的任一项是它后面第五项的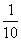 ,
,
(3)这个数列的任意两项的积仍在这个数列中。
证:(1)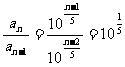 (常数)∴该数列成GP。
(常数)∴该数列成GP。
(2)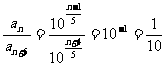 ,即:
,即: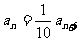 。
。
(3)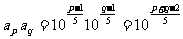 ,∵
,∵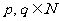 ,∴
,∴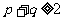 。
。
∴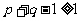 且
且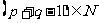 ,∴
,∴ ,(第
,(第 项)。
项)。
例三:设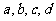 均为非零实数,
均为非零实数,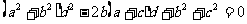 ,
,
求证: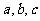 成GP且公比为
成GP且公比为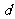 。
。
证一:关于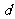 的二次方程
的二次方程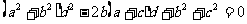 有实根,
有实根,
∴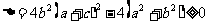 ,∴
,∴
则必有: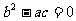 ,即
,即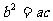 ,∴
,∴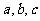 成GP
成GP
设公比为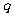 ,则
,则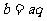 ,
,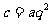 代入
代入
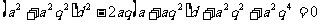
∵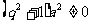 ,即
,即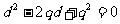 ,即
,即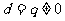 。
。
证二:∵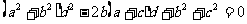
∴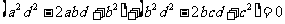
∴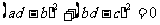 ,∴
,∴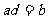 ,且
,且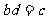
∵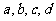 非零,∴
非零,∴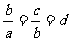 。
。
3、在等比数列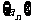 中,
中,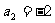 ,
,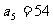 ,求
,求 ,
,
解: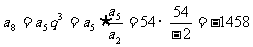
另解:∵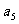 是
是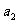 与
与 的等比中项,∴
的等比中项,∴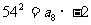
∴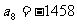
2、在等比数列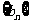 中,
中,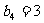 ,求该数列前七项之积。
,求该数列前七项之积。
解: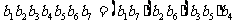
∵ ,∴前七项之积
,∴前七项之积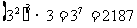
2、若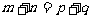 ,则
,则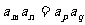 。
。
例一:1、在等比数列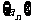 ,已知
,已知 ,
,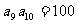 ,求
,求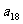 。
。
解:∵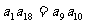 ,∴
,∴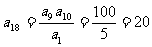
1、与首末两项等距离的两项积等于首末两项的积。
与某一项距离相等的两项之积等于 这一项的平方。
2、处理课本P128练习,重点是第三题。
《课课练》课时10 组合四
2.组合的应用:分清是否要排序.
例1.100件产品中有合格品90件,次品10件,现从中抽取4件检查.
⑴ 都不是次品的取法有多少种?
⑵ 至少有1件次品的取法有多少种?
⑶ 不都是次品的取法有多少种?
解:⑴ 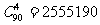 ;
;
⑵ 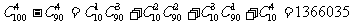 ;
;
⑶ 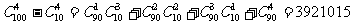 .
.
例2.从编号为1,2,3,…,10,11的共11个球中,取出5个球,使得这5个球的编号之和为奇数,则一共有多少种不同的取法?
解:分为三类:1奇4偶有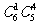 ;3奇2偶有
;3奇2偶有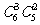 ;5奇1偶有
;5奇1偶有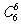
所以一共有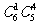 +
+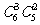 +
+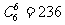 .
.
例3.现有8名青年,其中有5名能胜任英语翻译工作;有4名青年能胜任德语翻
译工作(其中有1名青年两项工作都能胜任),现在要从中挑选5名青年承担一项任务,其中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
解:我们可以分为三类:
① 让两项工作都能担任的青年从事英语翻译工作,有 ;
;
② 让两项工作都能担任的青年从事德语翻译工作,有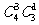 ;
;
③ 让两项工作都能担任的青年不从事任何工作,有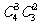 .
.
所以一共有 +
+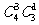 +
+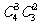 =42种方法.
=42种方法.
例4.甲、乙、丙三人值周,从周一至周六,每人值两天,但甲不值周一,乙不值周六,问可以排出多少种不同的值周表 ?
解法一:(排除法)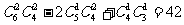
解法二:分为两类:一类为甲不值周一,也不值周六,有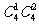 ;另一类为甲不值周一,但值周六,有
;另一类为甲不值周一,但值周六,有 .所以一共有
.所以一共有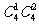 +
+ =42种方法.
=42种方法.
例5.6本不同的书全部送给5人,每人至少1本,有多少种不同的送书方法?
解:第一步从6本不同的书中任取2本“捆绑”在一起看成一个元素有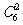 种方法;第二步将5个“不同元素(书)”分给5个人有
种方法;第二步将5个“不同元素(书)”分给5个人有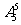 种方法.根据分步计数原理,一共有
种方法.根据分步计数原理,一共有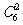
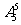 =1800种方法.
=1800种方法.
变题1:6本不同的书全部送给5人,有多少种不同的送书方法?
变题2: 5本不同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
变题3: 5本相同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
答案:1.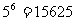 ; 2.
; 2.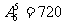 ; 3.
; 3.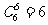 .
.
3.练习:处理《教学与测试》76课例题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com