
6、设直线l1、l2的倾斜角分别为θ1、θ2,斜率分别为k1、k2,且θ1+θ2=90°,则k1+k2的最小值是 .
5、光线由点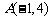 射出,遇到直线
射出,遇到直线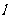 :
: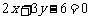 后被反射,并经过B
后被反射,并经过B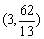 ,则反射光线所在直线的方程为
.
,则反射光线所在直线的方程为
.
4、函数f(θ)=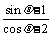 的最大值为
,最小值为 .
的最大值为
,最小值为 .
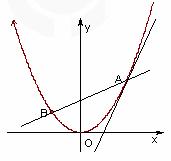
3、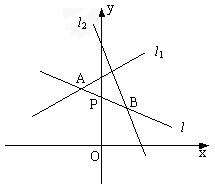 如图所示,已知直线l过点P(0,1)并与直线l1:x-3y+10=0和直线l2:2x+y-8=0分别交于A、B两点,若线段AB被点P平分,则直线l的方程为
.
如图所示,已知直线l过点P(0,1)并与直线l1:x-3y+10=0和直线l2:2x+y-8=0分别交于A、B两点,若线段AB被点P平分,则直线l的方程为
.
2、若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),则实数m的取值范围是 .
例1、过点P(2,1)的直线分别与x轴和y轴的正半轴交于A、B两点.求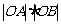 取得最小值时直线的方程.
取得最小值时直线的方程.
解:设直线的方程为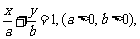
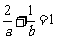 .
.
∴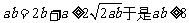 , ∴
, ∴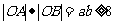 ,即
,即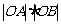 的最小值为8
的最小值为8
当且仅当a=2b,即a=4,b=2时取得等号。故所求直线的方程为:x+2y-4=0.
变式:过点P(2,1)的直线分别与x轴和y轴的正半轴交于A、B两点.求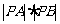 取得最小值时直线的方程.
取得最小值时直线的方程.
解:显然直线的斜率存在,设其方程为:y-1=k(x-2),则A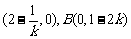
由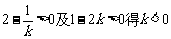 ,∴
,∴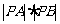 =
=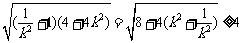
当且仅当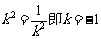 时取等号,∴
时取等号,∴ 的最小值为4时直线的方程为x+y-3=0.
的最小值为4时直线的方程为x+y-3=0.
例2、已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
|
|
甲 |
乙 |
丙 |
|
维生素A(单位/千克) |
600 |
700 |
400 |
|
维生素B(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
(Ⅰ)用x,y表示混合食物成本c元;
(Ⅱ)确定x,y,z的值,使混合物的成本最低.
解:(Ⅰ)由题,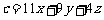 ,又
,又 ,所以
,所以 .
.
(Ⅱ)由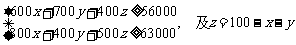 得,
得,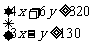 ,
,
所以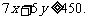 所以当且仅当
所以当且仅当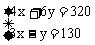 ,即
,即 时等号成立.
时等号成立.
 所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
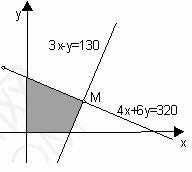
点评:本题为线性规划问题,用解析几何的观点看,问题的解实际上是由四条直线所围成的区域 上使得
上使得 最大的点.不难发现,应在点M(50,20)处取得.
最大的点.不难发现,应在点M(50,20)处取得.
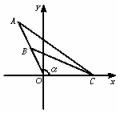
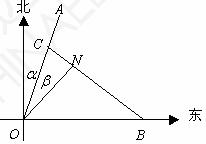 例3、如图,一列载着危重病人的火车从O地出发,沿射线OA的方向行驶,其中
例3、如图,一列载着危重病人的火车从O地出发,沿射线OA的方向行驶,其中 .在距离O地
.在距离O地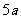 (
(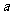 为正常数)千米、北偏东
为正常数)千米、北偏东 角的N处住有一位医学专家,其中
角的N处住有一位医学专家,其中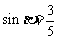 .现120指挥中心紧急调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往载有危重病人的火车,并在C处相遇。经测算,当两车行驶的路线与OB所围成的
.现120指挥中心紧急调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往载有危重病人的火车,并在C处相遇。经测算,当两车行驶的路线与OB所围成的 面积S最小时,抢救最及时.
面积S最小时,抢救最及时.
(1)在以O为原点,正北方向为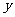 轴的平面直
轴的平面直
角坐标系中,求射线OA所在的直线方程;
(2)求S关于p的函数关系式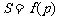 ;
;
(3)当p为何值时,抢救最及时?
解:(1)由 得
得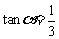 ,所以直线
,所以直线
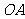 的方程为
的方程为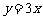 .
.
(2)设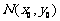 ,则
,则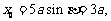
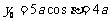 ,所以
,所以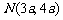 .
.
又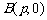 ,所以直线
,所以直线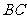 的方程为
的方程为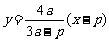 .
.
由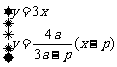 得C的纵坐标
得C的纵坐标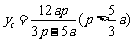 .
.
所以 的面积
的面积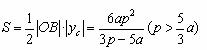
(3)由(2) ,因为
,因为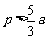 ,
,
所以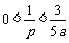 .
.
 所以
所以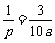 时,
时,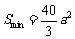 ,所以当
,所以当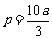 千米时,抢救最及时.
千米时,抢救最及时.
例4、某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为α(90°≤α<180°)的镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b).问学生距离镜框下缘多远看画的效果最佳?
解:建立如图所示的直角坐标系,AO为镜框边,AB为画的宽度,O为下边缘上的一点,在x轴的正半轴上找一点C(x,0)(x>0),欲使看画的效果最佳,应使∠ACB取得最大值.
由三角函数的定义知:A、B两点坐标分别为(acosα,asinα)、
(bcosα,bsinα),于是直线AC、BC的斜率分别为:
kAC=tan∠xCA=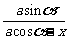 ,
,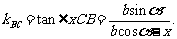
于是tan∠ACB=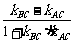

由于∠ACB为锐角,且x>0,则tan∠ACB≤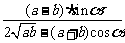 ,当且仅当
,当且仅当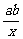 =x,
=x,
即x=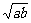 时,等号成立,此时∠ACB取最大值,对应的点为C(
时,等号成立,此时∠ACB取最大值,对应的点为C(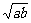 ,0),因此,学生距离镜框下缘
,0),因此,学生距离镜框下缘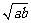 cm处时,视角最大,即看画效果最佳.
cm处时,视角最大,即看画效果最佳.
例5、在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示).将矩形折叠,使A点落在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
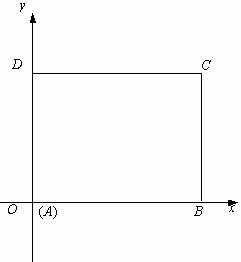 (Ⅱ)求折痕的长的最大值.
(Ⅱ)求折痕的长的最大值.
解:(I)(1)当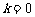 时,此时A点与D点重合, 折痕所在的直线方程
时,此时A点与D点重合, 折痕所在的直线方程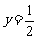 .
.
|
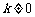 时,将矩形折叠后A点落在线段CD上的点为G(a,1)所以A与G关于折痕
时,将矩形折叠后A点落在线段CD上的点为G(a,1)所以A与G关于折痕
所在的直线对称,有
故G点坐标为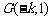 ,从而折痕所在的直线与OG
,从而折痕所在的直线与OG
的交点坐标(线段OG的中点)为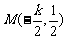 ,折痕
,折痕
所在的直线方程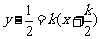 ,即
,即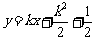 .
.
由(1)(2)得折痕所在的直线方程为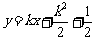 .
.
(II)折痕所在的直线与坐标轴的交点坐标为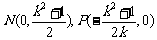 ,解
,解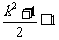 得
得
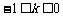 ;解
;解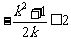 得
得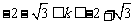 ,当A与D重合时,k= -2.
,当A与D重合时,k= -2.
(1)当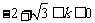 时,直线交BC于
时,直线交BC于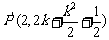 ,
,
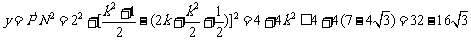 .
.
(2)当 时,
时,
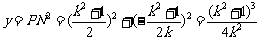 ,
,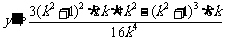
令 解得
解得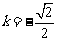 , 此时
, 此时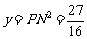 ,∴
,∴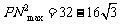 .
.
(3)当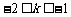 时,直线交DC于
时,直线交DC于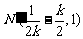
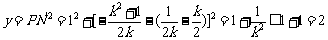
所以折痕的长度的最大值为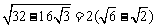 .
.
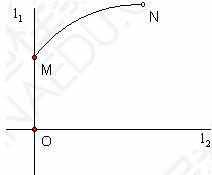 例6、如图所示,
例6、如图所示, 是通过城市开发区中心O的两条南北和东西走向的街道,连接
是通过城市开发区中心O的两条南北和东西走向的街道,连接 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在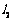 上的一段圆弧.若点M在点O正北方向,且
上的一段圆弧.若点M在点O正北方向,且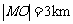 ,点N到
,点N到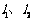 的距离分别为4km,5km.
的距离分别为4km,5km.
(1)建立适当的坐标系,求铁路线所在圆弧的方程.
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于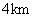 ,并且铁路上任意一点到校址的距离不能少于
,并且铁路上任意一点到校址的距离不能少于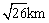 ,求该校址距点O的最近距离.(校址视为一个点)
,求该校址距点O的最近距离.(校址视为一个点)
解:(1)分别以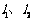 为
为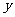 轴和
轴和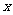 轴建立坐标系,由已知得
轴建立坐标系,由已知得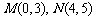 ,故
,故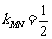 ,又线段
,又线段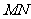 的中点为
的中点为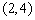 ,所以线段MN的垂直平分线的方程为
,所以线段MN的垂直平分线的方程为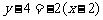 ,令
,令 得
得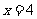 ,故圆心
,故圆心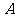 的坐标为
的坐标为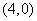 ,半径
,半径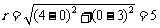 ,因此所求的圆
,因此所求的圆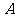 的方程为
的方程为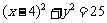 ,故有所求圆弧的方程为
,故有所求圆弧的方程为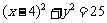
 .
.
(2)设校址选在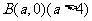 ,则
,则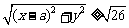 对
对 恒成立,
恒成立,
即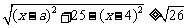 对
对 恒成立,整理得
恒成立,整理得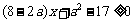
 对
对 恒成立,令
恒成立,令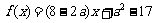 ,由
,由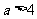 可得
可得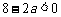 ,所以
,所以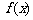 在区间
在区间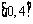 上为减函数,要使得
上为减函数,要使得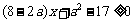 ,当且仅当
,当且仅当 和
和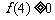 ,
,
即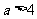 和
和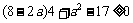 ,解之得
,解之得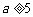 ,即校址应选在距
,即校址应选在距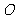 点最近
点最近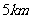 的地方。
的地方。
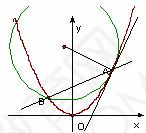
例7、已知抛物线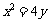 ,作直线
,作直线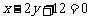 与抛物线交于
与抛物线交于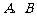 两点如图所示,过
两点如图所示,过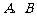 两点的圆与抛物线在
两点的圆与抛物线在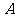 点处有相同的切线,求圆的方程.
点处有相同的切线,求圆的方程.
点拨:两曲线的交点能求出来,同时点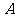 处的切线也可以应用导数求解,圆心在过
处的切线也可以应用导数求解,圆心在过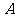 点垂直于此切线的直线上,并且也在弦
点垂直于此切线的直线上,并且也在弦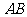 的垂直平分线上,故圆心和半径均亦确定。
的垂直平分线上,故圆心和半径均亦确定。
解:由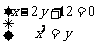 可得
可得 或者
或者
即 ,再由
,再由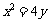 得
得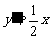 ,所以有
,所以有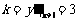 ,
,
 设圆的方程:
设圆的方程: ,圆的圆心为
,圆的圆心为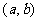 ,
,
则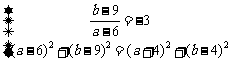 ,
,
解得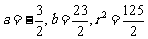 ,
,
所以所求的圆的方程为 .
.
例8、已知在平面直角坐标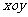 中,向量
中,向量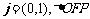 的面积为
的面积为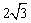 ,且
,且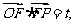
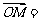
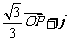 ,已知P点在第一象限内.
,已知P点在第一象限内.
(Ⅰ)设 求向量
求向量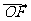 与
与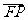 的夹角
的夹角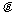 的取值范围;
的取值范围;
(Ⅱ)设以原点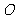 为中心,对称轴在坐标轴上,以
为中心,对称轴在坐标轴上,以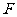 为右焦点的椭圆经过点
为右焦点的椭圆经过点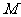 ,且
,且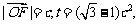 当
当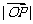 取最小值时,求椭圆方程.
取最小值时,求椭圆方程.
解析:(Ⅰ)由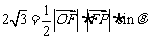 得
得
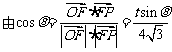 得
得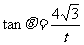
 ,
,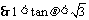 ,又
,又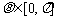 ,故夹角
,故夹角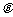 的取值范围为
的取值范围为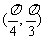 .
.
(Ⅱ)设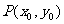 则
则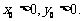 由(Ⅰ)知
由(Ⅰ)知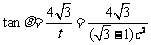
又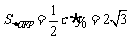 ,
,
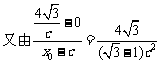 ,得
,得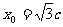
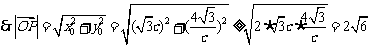
当且仅当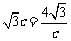 ,即c=2时,
,即c=2时,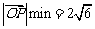 ,
,
此时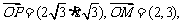
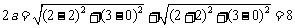
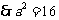 、
、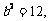 故所求椭圆方程为
故所求椭圆方程为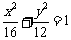
例9、椭圆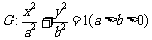 的两个焦点为
的两个焦点为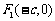 、
、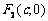 ,M是椭圆上一点,且满足
,M是椭圆上一点,且满足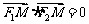
(Ⅰ)求离心率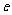 的取值范围;
的取值范围;
(Ⅱ)当离心率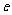 取得最小值时,点
取得最小值时,点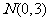 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为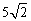 .
.
①求此时椭圆G的方程;
②设斜率为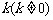 的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点
的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点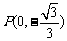 、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
解析:(Ⅰ)设点M的坐标为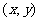 ,则
,则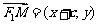 ,
,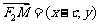
由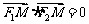 得
得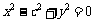 ,即
,即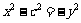 ①
①
又由点M在椭圆上,得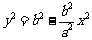 ,代入①
,代入①
得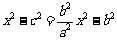 ,即
,即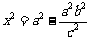

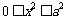 ,∴
,∴ 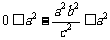
即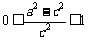 ,
, ,解得
,解得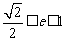
又
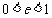 ,∴
,∴ 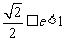 .
.
(Ⅱ)①当离心率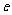 取最小值
取最小值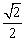 时,椭圆方程可表示为
时,椭圆方程可表示为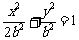
设点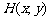 是椭圆上的一点,则
是椭圆上的一点,则
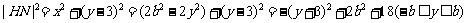
若0<b<3,则
当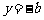 时,
时,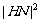 有最大值
有最大值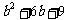 ,
,
由题意知: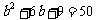 ,
,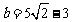 或
或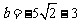 ,这与0<b<3矛盾.
,这与0<b<3矛盾.
若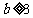 ,则
,则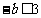
当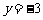 时,
时,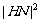 有最大值
有最大值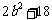
由题意知: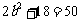 ,
,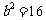 ,符合题意
,符合题意
∴所求椭圆G的方程为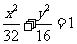
②设直线l的方程为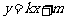 ,
,
代入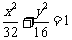 中,得
中,得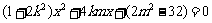
由直线l与椭圆G相交于不同的两点知
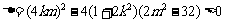
∴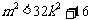 <1>
<1>
要使A、B两点关于过点P、Q的直线对称,必须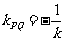
设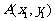 、
、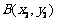 ,则
,则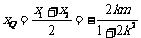 ,
,

 ,∴
,∴ ,∴
,∴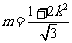 <2>
<2>
由<1>、<2>得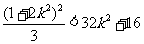 ,∴
,∴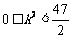 ,
,
又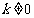 ,∴
,∴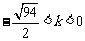 或
或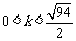
故当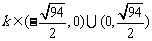 时,A、B两点关于过点P、Q的直线对称.
时,A、B两点关于过点P、Q的直线对称.
例10、已知双曲线的中心在原点O,右焦点为F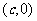 ,P是双曲线右支上一点,且
,P是双曲线右支上一点,且 的面积为
的面积为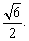
(Ⅰ)若点P的坐标为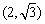 ,求此双曲线的离心率;
,求此双曲线的离心率;
(Ⅱ)若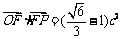 ,当
,当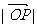 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
解析:(Ⅰ)设所求的双曲线的方程为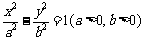 ,
,
由
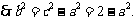
由点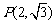 在双曲线上,
在双曲线上,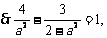 解得
解得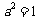 ,
,
∴离心率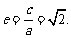
(Ⅱ)设所求的双曲线的方程为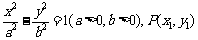 ,则
,则
∵△OFP的面积为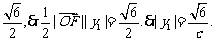
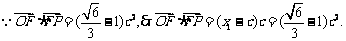 解得
解得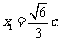
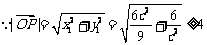 ,当且仅当
,当且仅当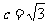 时等号成立.
时等号成立.
此时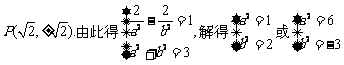 (舍)
(舍)
则所求双曲线的方程为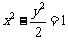 .
.
例11、某地政府为科技兴市,欲将如图甲所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知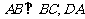 ∥
∥ 且
且 km,曲线段DC是以点D为顶点且开口向右的抛物线的一段.
km,曲线段DC是以点D为顶点且开口向右的抛物线的一段.
(Ⅰ)建立适当的坐标系,求曲线段DC的方程;
(Ⅱ)如果要使矩形的相邻两边分别落在AB、BC
上,且一个顶点落在DC上,问如何规划才能使矩形
工业园区的用地面积最大?并求出最大的用地面积.
(精确到0.1km2)

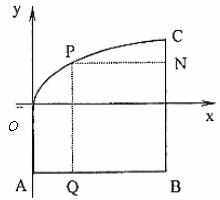
甲 乙
解析:(Ⅰ)以D为原点,DA所在直线为y轴建立直角坐标系如图乙,依题意可设抛物线方程为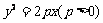 ,且C(4,2).
,且C(4,2).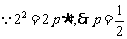 .故曲线段DC的方程为
.故曲线段DC的方程为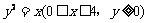 .
.
(Ⅱ)设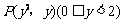 是曲线段DC上的任意
是曲线段DC上的任意
则在矩形PQBN中,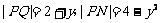 .
.
 工业区面积
工业区面积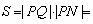
 .
.
又 ,令
,令 得
得 。
。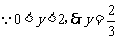 .
.
当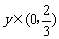 时,
时, ,S是y的增函数;当
,S是y的增函数;当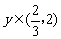 时,
时, ,S是y的减函数.
,S是y的减函数.  时,S取到极大值,此时
时,S取到极大值,此时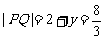 .
.
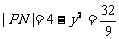 ,故
,故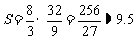 .
.
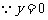 时
时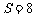 ,
,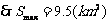 .
.
答:当矩形的长为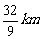 ,宽为
,宽为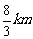 时,园区的用地面积最大,约为
时,园区的用地面积最大,约为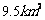 .
.
[模拟试题]
1、设直线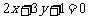 和圆
和圆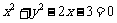 相交于点A、B,则弦AB的垂直平分线方程是
.
相交于点A、B,则弦AB的垂直平分线方程是
.
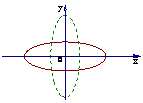
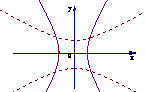
(三)圆锥曲线
|
名 称 |
椭
圆 |
双 曲 线 |
|
图 象 |
 |
 |
|
定 义 |
平面内到两定点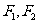 的距离的和为常数(大于 的距离的和为常数(大于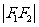 )的动点的轨迹叫椭圆 )的动点的轨迹叫椭圆 即 即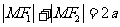 当2 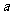 ﹥2 ﹥2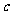 时,轨迹是椭圆, 时,轨迹是椭圆,当2 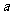 =2 =2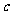 时,轨迹是一条线段 时,轨迹是一条线段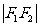 当2 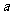 ﹤2 ﹤2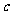 时,轨迹不存在 时,轨迹不存在 |
平面内到两定点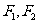 的距离的差的绝对值为常数(小于 的距离的差的绝对值为常数(小于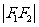 )的动点的轨迹叫双曲线 )的动点的轨迹叫双曲线 即 即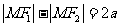 当2 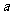 ﹤2 ﹤2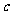 时,轨迹是双曲线 时,轨迹是双曲线当2 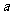 =2 =2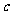 时,轨迹是两条射线 时,轨迹是两条射线当2 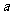 ﹥2 ﹥2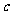 时,轨迹不存在 时,轨迹不存在 |
|
标 准 方 程 |
焦点在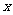 轴上时: 轴上时: 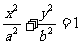 焦点在  轴上时: 轴上时: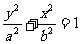 |
焦点在 轴上时: 轴上时: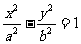 焦点在 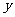 轴上时: 轴上时: |
常数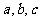 的关系 |
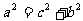 , ,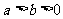 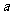 最大,可以 最大,可以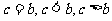 |
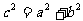 , ,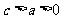 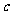 最大,可以 最大,可以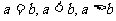 |
|
渐 近 线 |
|
焦点在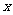 轴上时: 轴上时: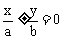 焦点在 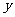 轴上时: 轴上时: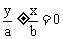 |
抛物线:
|
图形 |
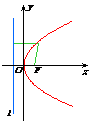 |
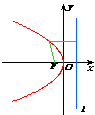 |
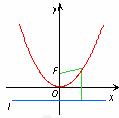 |
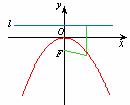 |
|
方程 |
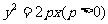 |
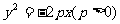 |
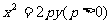 |
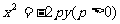 |
|
焦点 |
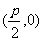 |
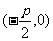 |
 |
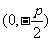 |
|
准线 |
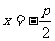 |
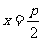 |
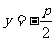 |
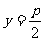 |
(二)圆的方程
(1)圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆
(2)圆的标准方程
: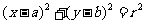 圆心为
圆心为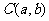 ,半径为
,半径为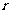 ,
,
(3)圆的一般方程:
只有当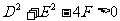 时,
时,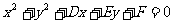 ①表示的曲线才是圆,把形如①的方程称为圆的一般方程
①表示的曲线才是圆,把形如①的方程称为圆的一般方程
(1)当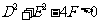 时,①表示以(-
时,①表示以(-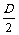 ,-
,-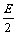 )为圆心,
)为圆心, 为半径的圆;
为半径的圆;
(2)当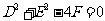 时,方程①只有实数解
时,方程①只有实数解 ,
,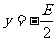 ,即只表示一个点(-
,即只表示一个点(-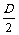 ,-
,-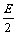 );
);
(3)当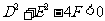 时,方程①没有实数解,因而它不表示任何图形。
时,方程①没有实数解,因而它不表示任何图形。
(一)直线方程
|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
示意图 |
|
点斜式 |
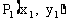 ,k ,k |
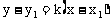 |
k存在 |
|
|
斜截式 |
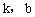 |
 |
k存在 |
|
|
两点式 |
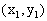 ( (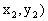 |
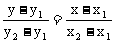 |
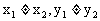 |
|
|
截距式 |
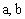 |
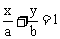 |
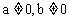 |
|
|
一般式 |
|
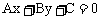 |
A、B不全为0 |
|
P128-129课时8中 例一,例二,例三,练习5,6,7,8。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com