
7. I'd come to if 1 had time to spare.
6. He has no choice but to cry.
5. It's silly of sb. to do sth.
4. You shall get justice.
3. I never knew so young a body with so wise a head.
2. I offer you six times what you have just offered.
1. She dressed herself as a lawyer's clerk.
20.(本小题满分12分)
已知函数f(x)= ax,g(x)= lnx-2.
(1) 试讨论这两个函数的图像的交点个数.
(2) 当a=1时,令h(x)=f(x)-g(x),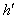 (x)为函数h(x)的导数,求证:对任意实数m,n,当0<m<n时,关于x的方程
(x)为函数h(x)的导数,求证:对任意实数m,n,当0<m<n时,关于x的方程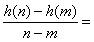
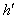 (x)在区间[m,n]恒有实数解.
(x)在区间[m,n]恒有实数解.
解:(1)令F(x)=f(x)-g(x), 由已知F(x)的定义域为{x|x>0},
由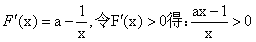
当a>0时,解得:x<0(舍去)或x> ,-----2分 由
,-----2分 由
|
x |
(0,  ) ) |
 |
( ,
+∞) ,
+∞) |
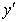 |
- |
0 |
+ |
|
y |
↘ |
极小值 3+lna |
↗ |
-------3分
① 当3+lna>0,即a>e-3时,F(x)>0恒成立,F(x)无零点.-----4分
② 当0<a< e-3时,F(x)的极小值3+lna<0,又当x→0时,F(x)=ax-lnx+2→+∞,F(1)=a+2>0,故F(x)有两个零点.-----5分
当a=0时,F(x)=-lnx+2为减函数,F(x)有且只有一个零点e2
当a<0时,F(x)=ax-lnx+2亦为减函数,且当x→0时,F(x)=ax-lnx+2→+∞,当x→+∞时,F(x)→-∞,故F(x)有且只有一个零点.
当a= e-3时,3+lna=0,F(x)只有一个零点. -----7分
综上所述,当a> e-3时,这两函数的图像无交点;当0<a< e-3时这两函数图像有两个交点;当a≤0或a= e-3时,这两函数有且只有一个交点.----8分
(2)依题意: 方程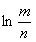 -
-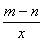 =0在区间[m,n]内有解.故只须证明
=0在区间[m,n]内有解.故只须证明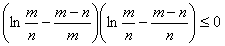 即可.-------9分
即可.-------9分
令s(x)=ln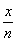 -
-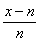 ,x∈[m,n],则
,x∈[m,n],则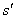 (x)=
(x)=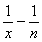 >0(∵m<x<n),故函数s(x)在[m,n]为增函数,故s(m)<s(n)=0,即
>0(∵m<x<n),故函数s(x)在[m,n]为增函数,故s(m)<s(n)=0,即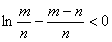 ;-------10分
;-------10分
令t(x)=ln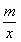 -
-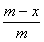 x∈[m,n],则
x∈[m,n],则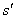 (x)=
(x)=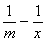 >0(∵m<x<n),故函数t(x)在[m,n]为增函数,即t(n)>t(m)=0,即
>0(∵m<x<n),故函数t(x)在[m,n]为增函数,即t(n)>t(m)=0,即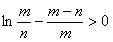 ;故
;故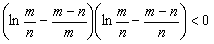 ,--11分
,--11分
综上所述,当0<m<n时,关于x的方程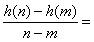
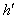 (x)在区间[m,n]恒有实数解.---12分
(x)在区间[m,n]恒有实数解.---12分
19.(本小题满分14分)
已知函数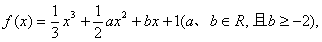 当
当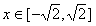 时,总有
时,总有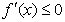 .
.
(1)求函数f(x)的解析式;
(2)设函数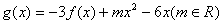 ,求证:当
,求证:当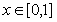 时,若
时,若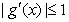 恒成立,则|g(x)|≤3.5也恒成立.
恒成立,则|g(x)|≤3.5也恒成立.
解:(1)由条件,得 ,……………1分
,……………1分
当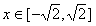 时,总有
时,总有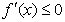 ,所以有
,所以有

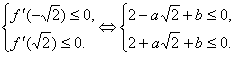
由①+②得,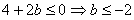 ,
,
又b≥-2,∴b=-2,…………………………………………………………4分
把b=-2代入①和②得
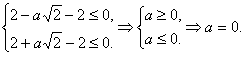
因此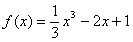 .…………………………………………………7分
.…………………………………………………7分
(2)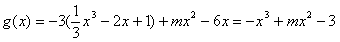 ,
,
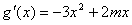 是关于x的二次函数,……………………………8分
是关于x的二次函数,……………………………8分
当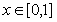 时,
时,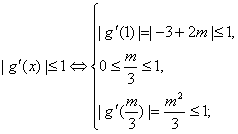 或
或
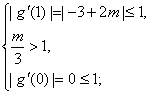 或
或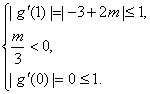 ------11分
------11分
解得,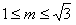 . 因此,当
. 因此,当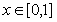 时,
时,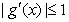 的恒成立,则
的恒成立,则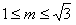 ------12分
------12分
由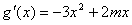 >0(0≤x≤1)可知,当1≤m≤
>0(0≤x≤1)可知,当1≤m≤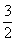 时g(x)在[0,
时g(x)在[0, 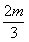 ]为增函数,在[
]为增函数,在[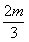 ,1]上为减函数|,|g(0)|=3≤3.5,|g(1)|=|m-4|≤3,|g(
,1]上为减函数|,|g(0)|=3≤3.5,|g(1)|=|m-4|≤3,|g(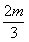 )|=|
)|=|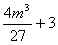 |≤3.5,即|g(x)|≤3.5;---13分
|≤3.5,即|g(x)|≤3.5;---13分
当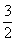 ≤m≤
≤m≤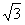 时g(x)在[0,1]为增函数,|g(0)|=3≤3.5,|g(1)|=|m-4|≤2.5,即|g(x)|≤3.5。综上所述,当
时g(x)在[0,1]为增函数,|g(0)|=3≤3.5,|g(1)|=|m-4|≤2.5,即|g(x)|≤3.5。综上所述,当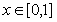 时,若
时,若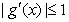 恒成立,则|g(x)|≤3.5也恒成立.---14分
恒成立,则|g(x)|≤3.5也恒成立.---14分
18.(本小题满分14分)
在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由.
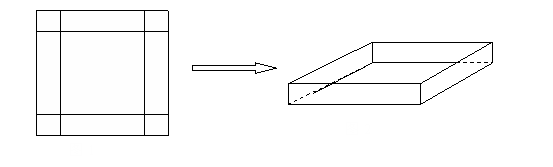
解:(1)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x ,
所以V1= (4-2x)2·x = 4(x3-4x2 + 4x) (0<x<2) .……….. ……….. ……….. 4分
∴V1/ = 4(3x2-8x + 4),……….. ……….. ……….. ……….. ……….. ………. ….5分
令V1/ = 0,即4(3x2-8x + 4) = 0,解得x1 = 3,x2 = 2 (舍去) .……….. ………7分
∵ V1在(0,2)内只有一个极值,
∴ 当x = 3时,V1取得最大值27.27<5,即不符合要求. ….…. …. 9分
(2)重新设计方案如下:
如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;如图③,将图②焊成长方体容器.新焊长方体容器底面是一个长方形,长为3,宽为2,此长方体容积V2 = 3×2×1 = 6,显然V2>5.
故第二种方案符合要求.
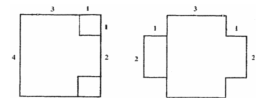
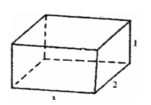
图① 图② 图③
…. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. ….14分
注:第二问答案不唯一。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com