
53.
 (2009南州)已知二次函数
(2009南州)已知二次函数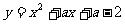 。
。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为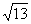 时,求出此二次函数的解析式。
时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为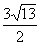 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
51. (2009衡阳)如图12,直线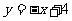 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为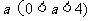 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与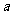 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.


52. (2009娄底)如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH
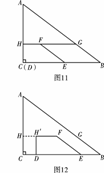 (HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3
(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3
(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个
单位的速度沿CB方向向右移动,直到点D与点B
重合时停止,设运动的时间为t秒,运动后的直角梯
形为DEFH′(如图12).
探究1:在运动中,四边形CDH′H能否为正方形?若能,
请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,△ABC与直角梯形DEFH′重叠
部分的面积为y,求y与t的函数关系.?
49.
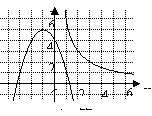
(2009嘉兴)如图,曲线C是函数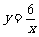 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数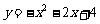 的图象.点
的图象.点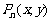 (
(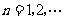 )在曲线C上,且
)在曲线C上,且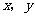 都是整数.
都是整数.
(1)求出所有的点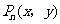 ;
;
(2)在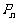 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
48.
(本题满分13分)(2009宁德)如图,已知抛物线C1: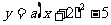 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求P点坐标及a的值;(4分)
(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;(4分)
 (3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.(5分)
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.(5分)

47. (2009丽水)已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
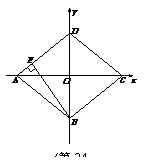 (1)填空:菱形ABCD的边长是 ▲ 、面积是
▲ 、
(1)填空:菱形ABCD的边长是 ▲ 、面积是
▲ 、
高BE的长是 ▲ ;
(2)探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k
个单位,在运动过程中,任何时刻都有相应的k值,使得
△APQ沿它的一边翻折,翻折前后两个三角形组成的四边
形为菱形.请探究当t=4秒时的情形,并求出k的值.
46. (2009深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
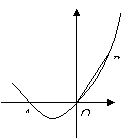 (1)求点B的坐标;
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
45. (2009南充)如图9,已知正比例函数和反比例函数的图象都经过点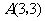 .
.
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点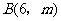 ,求
,求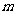 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与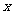 轴、
轴、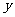 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
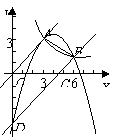 (4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积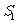 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: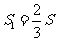 ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
44.
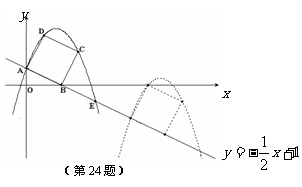
 (2009台州)如图,已知直线 交坐标轴于
(2009台州)如图,已知直线 交坐标轴于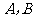 两点,以线段
两点,以线段 为边向上作
为边向上作
正方形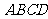 ,过点
,过点 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为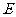 .
.
(1)请直接写出点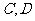 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒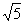 个单位长度的速度沿射线
个单位长度的速度沿射线 下滑,直至顶点
下滑,直至顶点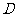 落在
落在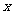 轴上时停止.设正方形落在
轴上时停止.设正方形落在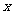 轴下方部分的面积为
轴下方部分的面积为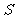 ,求
,求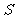 关于滑行时间
关于滑行时间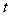 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量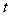 的取值范围;
的取值范围;
 (4)在(3)的条件下,抛物线与正方形一起平移,同时
(4)在(3)的条件下,抛物线与正方形一起平移,同时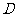 停止,求抛物线上
停止,求抛物线上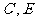 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.

43.
(2009重庆) (2009重庆已知:如图,在平面直角坐标系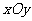 中,矩形OABC的边OA在
中,矩形OABC的边OA在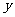 轴的正半轴上,OC在
轴的正半轴上,OC在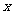 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
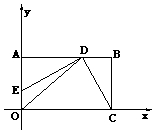 (1)求过点E、D、C的抛物线的解析式;
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与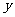 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为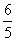 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com