11．两个等比数列{a_n}与{b_n}的积、商、倒数组成的数列

{a_nb_n}、、仍为等比数列。

10．两个等差数列{a_n}与{b_n}的和差的数列{a_n+b_n}、{a_n-b_n}仍为等差数列。

9．等比数列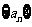中为　　　 数列，其中为前项的和。

8．等比数列{a_n}中，若m+n=p+q，则　　　　　　　　

7．等差数列{a_n}中，若m+n=p+q，则　　　　　　　　

6．等差数列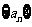中为　　　 数列，其中为前项的和。

4．等差中项和等比中项

如果在与中间插入一个数A，使得，A，成等差数列，那么A叫做与的　　　 ，则A＝　　　　　　 。

如果在与中间插入一个数C，使得，C，成等比数列，那么C叫做与的　　　 ，则C＝　　　　 。

3．等差数列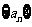的前项和公式为：　　　　　　 。等比数列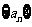的前项和公式为：　　　　　　 。(注意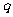：＝1与的分类讨论)

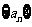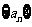2．等差数列的通项公式为：　　　　　 。等比数列的通项公式为：　　　　　 。

要求：理解等差、等比数列的概念，掌握等差、等比数列的通项公式与前项和公式，能在五个基本量中“知三求二”。掌握等差、等比数列两个公式的推导过程中所涉及的数学思想方法(如：“归纳猜想”“倒序相加”“错位相减”等)，用函数的思想理解等差、等比数列的通项公式与前项和公式，并能解决简单的实际问题。

1．等差、等比数列的概念

　　　　　 　　那么这个数列叫等差数列，常数叫做等差数列的　　　 ；

　　　　　 　　那么这个数列叫等比数列，常数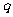叫做等比数列的　　　 。(注意)。