
 ⒖(12分)已知函数
⒖(12分)已知函数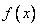 在定义域
在定义域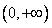 上为增函数,且满足
上为增函数,且满足 .
.
 (1)求
(1)求 的值;
(2)解不等式:
的值;
(2)解不等式: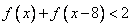 .
.
 ⒗(12分)已知
⒗(12分)已知 函数
函数 在
在 单调递增,
单调递增,

 关于
关于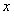 的不等式
的不等式
 的解集为
的解集为 ,
,
 若
若 为真命题,
为真命题,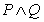 为假命题,求
为假命题,求 的取值范围.
的取值范围.


⒘(14分)设 的
的
 图象经过点
图象经过点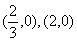 ,如右图所示。
,如右图所示。
 ⑴求函数
⑴求函数 的解析式和极值;
的解析式和极值;
 ⑵对
⑵对 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。


 ⒙(14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费方法是:水费=基本费+超额费+损耗费。该市规定:
⒙(14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费方法是:水费=基本费+超额费+损耗费。该市规定:
 ①若每月用水量不超过最低限量
①若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月的定额损耗费
立方米时,只付基本费9元和每户每月的定额损耗费 元;
元;
 ②若每月用水量超过
②若每月用水量超过 立方米时,除了付基本费和损耗费外,超过部分每立方米付
立方米时,除了付基本费和损耗费外,超过部分每立方米付

 元的超额费;
元的超额费;
 ③每户每月的损耗费
③每户每月的损耗费 不超过5元。
不超过5元。
 ⑴求每户每月水费
⑴求每户每月水费 (元)和用水量
(元)和用水量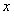 (立方米)的函数关系式;
(立方米)的函数关系式;
 ⑵该市一家庭去年第一季度的用水量和支付的费用如下表所示:
⑵该市一家庭去年第一季度的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一月份 |
4 |
17 |
|
二月份 |
5 |
23 |
|
三月份 |
2.5 |
11 |
试分析一、二、三各月份的用水量是否超过最低限量,并求 、
、 、
、 的值。
的值。
 ⒚(14分)已知函数
⒚(14分)已知函数 .
.
 ⑴当
⑴当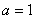 时,求过点
时,求过点 且与函数
且与函数 的图象相切的直线
的图象相切的直线 的方程;
的方程;
 ⑵设
⑵设 ,求
,求 的最大值
的最大值 的解析式.
的解析式.
 ⒛(14分)已知函数
⒛(14分)已知函数 为奇函数,当
为奇函数,当 时,
时,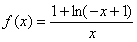 .
.
 ⑴求当
⑴求当 时,
时, 的表达式;
的表达式;
 ⑵对于任意
⑵对于任意 ,比较
,比较 与
与 的大小,证明你的结论;
的大小,证明你的结论;
⑶若对任意的 及
及 ,不等式
,不等式 恒成立,求正整数
恒成立,求正整数 的最大值。
的最大值。
39. (2009仙桃)“学雷锋活动日”这天,阳光中学安排七、八、九年级部分学生代表走出校园参与活动,活动内容有:A.打扫街道卫生;B.慰问孤寡老人;C.到社区进行义务文艺演出.学校要求一个年级的学生代表只负责一项活动内容.
(1)若随机选一个年级的学生代表和一项活动内容,请你用列表法(或画树状图)表示所有可能出现的结果;
(2)求九年级学生代表到社区进行义务文艺演出的概率.
38. (2009遂宁)在A、B两个盒子中都装着分别写有1-4的4张卡片,小明分别从A、B两个盒子中各取出一张卡片,并用A盒中卡片上的数字作为十位数,B盒中的卡片上的数字作为个位数.请画出树状图,求小明抽取一次所得两位数能被3整除的概率.
37. (本小题满分7分)
(2009衡阳)一个不透明口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色处没有任何其他区别现.从中任意摸出一个球.
(1)计算摸到的是绿球的概率.
(2)如果要使摸到绿球的概率为 ,需要在这个口袋中再放入多少个绿球?
,需要在这个口袋中再放入多少个绿球?
(2009烟台)将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是 ;
 (3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
36. (8分)(2009洛江)在一个布口袋中装有只有颜色不同,其它都相同的白、红、黑三种颜色的小球各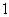 只,甲乙两人进行摸球游戏;甲先从袋中摸出一球看清颜色后放回,再由乙从袋中摸出一球.
只,甲乙两人进行摸球游戏;甲先从袋中摸出一球看清颜色后放回,再由乙从袋中摸出一球.
(1)试用树状图(或列表法)表示摸球游戏所有可能的结果;
(2)如果规定:乙摸到与甲相同颜色的球为乙胜,否则为负,试求乙在游戏中能获胜的概率.
35. (本题满分10分)
(2009安顺)下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的统计图表如下:
依据上列图表,回答下列问题:
(1) 其中观看足球比赛的门票有_____张;观看乒乓球比赛的门票占全部门票的_____%;
(2) 公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地完全相同且充分洗匀),问员工小华抽到男篮门票的概率是_____;
(3)
若购买乒乓球门票的总款数占全部门票总款数的 ,求每张乒乓球门票的价格。
,求每张乒乓球门票的价格。

34. (本小题满分12分)
(2009广州)有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别。现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球。
(1)请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况;
(2)求红球恰好被放入②号盒子的概率。
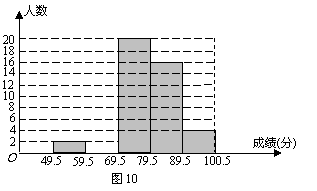
33. (2009益阳)某校数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图(图10). 请你根据图表提供的信息,解答下列问题:
(1) 频数、频率分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少?
|
分组 |
49.5~59.5 |
59.5~69.5 |
69.5~79.5 |
79.5~89.5 |
89.5~100.5 |
合计 |
|
频数 |
2 |
a |
20 |
16 |
4 |
50 |
|
频率 |
0.04 |
0.16 |
0.40 |
0.32 |
b |
1 |
32. 如图,(1),A、B两个转盘分别被分成三个、四个相同的扇形,分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止)。
(1) 用列表(或画树状图)的方法,求两个指针所指的区域内的数字之和大于7的概率。
(2) 如果将图(1)中的转盘改为图(2),其余不变,求两个指针所知区域的数字之和大于7 的概率。
31.  (本题满分8分)(2009江苏)一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是多少?
(本题满分8分)(2009江苏)一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com