
2.常见的排队的三种题型: ⑴某些元素不能在或必须排列在某一位置--优限法;
⑵某些元素要求连排(即必须相邻)--捆绑法;
⑶某些元素要求分离(即不能相邻)--插空法.
1.排列、排列数的定义,排列数的两个计算公式;
例4 椭圆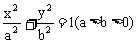 与x轴的正向相交于点A,O为坐标原点,若这个椭圆上存在点P,使得OP⊥AP。求该椭圆的离心率e的取值范围。
与x轴的正向相交于点A,O为坐标原点,若这个椭圆上存在点P,使得OP⊥AP。求该椭圆的离心率e的取值范围。

解:设椭圆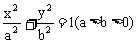 上的点P的坐标是(
上的点P的坐标是(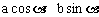 )(α≠0且α≠π),A(a,0)。
)(α≠0且α≠π),A(a,0)。
则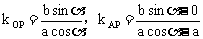 。而OP⊥AP,
。而OP⊥AP,
于是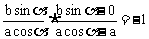 ,整理得
,整理得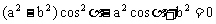
解得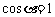 (舍去),或
(舍去),或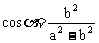 。
。
因为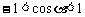 ,所以
,所以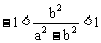 。可转化为
。可转化为 ,解得
,解得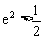 ,于是
,于是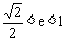 。故离心率e的取值范围是
。故离心率e的取值范围是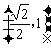 。
。
例3 设点P(x,y)在椭圆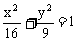 ,试求点P到直线
,试求点P到直线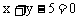 的距离d的最大值和最小值。
的距离d的最大值和最小值。
解:点P(x,y)在椭圆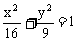 上,设点P(
上,设点P(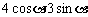 )(α是参数且
)(α是参数且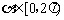 ),
),
则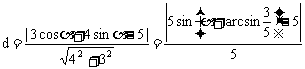 。
。
当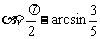 时,距离d有最小值0,此时椭圆
时,距离d有最小值0,此时椭圆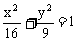 与直线
与直线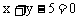 相切;当
相切;当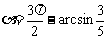 时,距离d有最大值2。
时,距离d有最大值2。
例2 已知点A在椭圆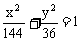 上运动,点B(0,9)、点M在线段AB上,且
上运动,点B(0,9)、点M在线段AB上,且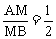 ,试求动点M的轨迹方程。
,试求动点M的轨迹方程。
解:由题意知B(0,9),设A( ),并且设M(x,y)。
),并且设M(x,y)。
则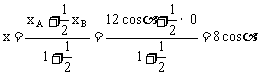
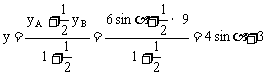 ,
,
动点M的轨迹的参数方程是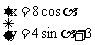 (α是参数),
(α是参数),
消去参数得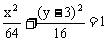 。
。
例1 求椭圆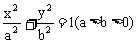 的内接矩形的面积及周长的最大值。
的内接矩形的面积及周长的最大值。
解:如图,设椭圆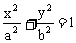 的内接矩形在第一象限的顶点是A(
的内接矩形在第一象限的顶点是A(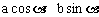 )(
)(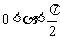 ),矩形的面积和周长分别是S、L。
),矩形的面积和周长分别是S、L。
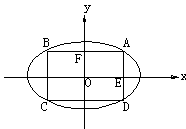
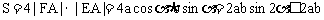 ,
,
当且仅当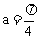 时,
时,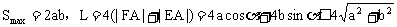 ,
,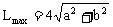 ,此时α存在。
,此时α存在。
(1)正弦定理: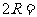 = =
= =
(2)余弦定理:

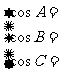
(3)S = =
=
= =
=
(4)解三角形的几种类型及步骤:
①已知两角一边:
先用 →再用 。
②已知两边及夹角:
先用 →再用 。
③已知两边及一边对角:
先用 (注意:解;内角和)
→再用 。
④已知三边:
先用 →再用 。
(5)解应用问题的一般步骤:① → ② → ③ → ④
注意:在运用正余弦定理时应注意三角公式的运用。(特别是半角,倍角,和角公式)还要注意切化弦的思想。
(1) 叫做向量。
(2)向量的运算:
|
运算 |
定义 或 法则 |
运算性质(运算律) |
坐标运算 |
|
加 法 |
    |
|
|
|
减 法 |
  |
|
|
|
实数与向量的积 |
|
|
|
|
数量积 |
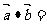 几何意义: |
|
|
(3)平面向量的基本定理:
如果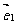 和
和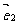 是同一平面内的两个不共线的向量,那么
。
是同一平面内的两个不共线的向量,那么
。
(4)两个向量平行和垂直的充要条件: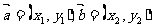
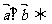
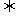 ;
;
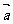 ∥
∥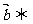
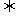 ;
;
(5)夹角、模、距离等计算:
夹角: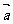 与
与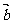 的夹角
的夹角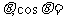
模: |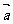 +
+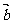 |=
|=
|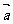 -
-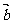 |=
|=
|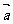 +
+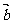 +
+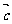 |=
|=
模|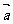 |= 两点距离公式:|P
|= 两点距离公式:|P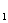 P
P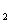 |=
向量|
|=
向量|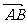 |=
|=
计算:求与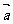 =(a,b)共线的单位向量
=(a,b)共线的单位向量
(6)线段的定比分点坐标公式:
设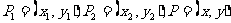 ,且
,且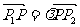 ,则
,则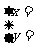
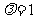 时,得中点坐标公式:
时,得中点坐标公式: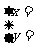 可推出三角形重心坐标公式:
可推出三角形重心坐标公式: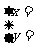
还应在已知三角形三顶点坐标的前提下会求中线,高线角平分线。
(7)平移公式
点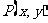 按
按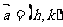 平移到
平移到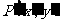 ,则
,则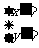
点( ) 点P(a,b)
点P(a,b)  点( )
点( )
曲线y=
 曲线y=f(x)
曲线y=f(x)  曲线y=
曲线y=
14.在△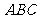 中,
中,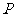 为形内一点,
为形内一点,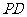 、
、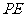 、
、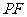 为
为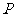 到三边
到三边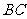 、
、 、
、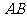 的距离,
的距离,
求证: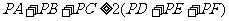
13.设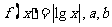 是满足
是满足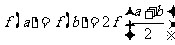 的实数,其中
的实数,其中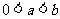 ;
;
(1)求证: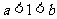 ;(2)求证:
;(2)求证:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com