
7.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180 个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销焦点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②,则完成①、②这两项调查宜采用的抽样方法依次是( )
(A)分层抽样,系统抽样法 (B)分层抽样法,简单随机抽样法
(C)系统抽样法,分层抽样法 (D)简随机抽样法,分层抽样法
6.将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上和概率是 ( )
(A) (B) (C) (D)
4.一台X型号的自动机床在一小时内不需要工人照看的概率为0.8000,有四台这种型号的自动机床各自独立工作,则一小时内至多有2台机床需要工人照看的概率是( )
(A)0.1536 (B)0.1808 (C)0.5632 (D)0.9728
3.在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有( )
A.56个 B.57个 C.58个 D.60个
2.从数字1,2,3,4,5,中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为( )
A.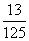 B.
B. C.
C.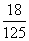 D.
D.
1.从1,2,……,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是( )
A. B.
B. C.
C.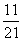 D.
D.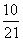
解: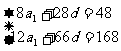


2°
已知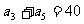 ,求
,求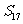 .
.
解:∵ ∴
∴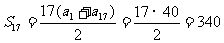
例二 已知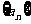 ,
,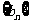 都成AP,且
都成AP,且 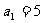 ,
, ,
,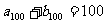 试求数
试求数
列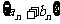 的前100项之和
的前100项之和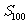 .
.
解:
例三 一个等差数列的前12项之和为354,前12项中偶数项与奇数项之比为32:27,求公差。
解一:设首项为 ,公差为
,公差为 则
则
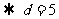
解二:
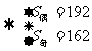 由
由 
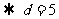
例四 已知: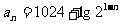 (
( )
)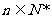 问多少项之和为最
问多少项之和为最
大?前多少项之和的绝对值最小?
解:1° 
 ∴
∴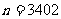
2° 
当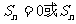 近于0时其和绝对值最小
近于0时其和绝对值最小
令: 即
1024+
即
1024+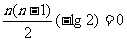
得:
∵ 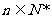 ∴
∴
例五 项数是 的等差数列,中央两项为
的等差数列,中央两项为 是方程
是方程 的
的
两根,求证此数列的和是方程 
的根。 (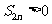 )
)
解:依题意:
∵ ∴
∴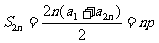
∵
∴  ∴
∴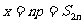 (获证)
(获证)
例六 (机动,作了解)求和
1° 
解:
∴ 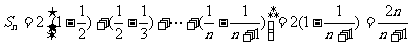
2° 
解:原式=
示例一: 从10个不同的文艺节目中选6个编成一个节目单,如果某女演员的独唱节目一定不能排在第二个节目的位置上,则共有多少种不同的排法?
解法一:(从特殊位置考虑)
解法二:(从特殊元素考虑)若选: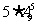 若不选:
若不选: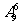
则共有
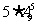 +
+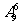 =136080
=136080
解法三:(间接法) 136080
136080
示例二:
⑴ 八个人排成前后两排,每排四人,其中甲、乙要排在前排,丙要排在后排,
则共有多少种不同的排法?
略解:甲、乙排在前排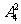 ;丙排在后排
;丙排在后排 ;其余进行全排列
;其余进行全排列 .
.
所以一共有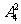

 =5760种方法.
=5760种方法.
⑵ 不同的五种商品在货架上排成一排,其中a, b两种商品必须排在一起,而c, d两种商品不排在一起, 则不同的排法共有多少种?
略解:(“捆绑法”和“插空法”的综合应用)a, b捆在一起与e进行排列有 ;
;
此时留下三个空,将c, d两种商品排进去一共有 ;最后将a, b“松绑”有
;最后将a, b“松绑”有 .所以一共有
.所以一共有

 =24种方法.
=24种方法.
☆⑶ 6张同排连号的电影票,分给3名教师与3名学生,若要求师生相间而坐,则不同的坐法有多少种?
略解:(分类)若第一个为老师则有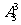
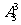 ;若第一个为学生则有
;若第一个为学生则有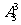
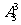
所以一共有2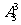
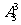 =72种方法.
=72种方法.
示例三:
⑴ 由数字1,2,3,4,5可以组成多少个没有重复数字的正整数?
略解:
⑵ 由数字1,2,3,4,5可以组成多少个没有重复数字,并且比13 000大的正整数?
解法一:分成两类,一类是首位为1时,十位必须大于等于3有 种方法;另一类是首位不为1,有
种方法;另一类是首位不为1,有 种方法.所以一共有
种方法.所以一共有
 个数比13 000大.
个数比13 000大.
解法二:(排除法)比13 000小的正整数有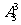 个,所以比13 000大的正整数有
个,所以比13 000大的正整数有
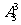 =114个.
=114个.
示例四: 用1,3,6,7,8,9组成无重复数字的四位数,由小到大排列.
⑴ 第114个数是多少? ⑵ 3 796是第几个数?
解:⑴
因为千位数是1的四位数一共有 个,所以第114个数的千位数应该是“3”,十位数字是“1”即“31”开头的四位数有
个,所以第114个数的千位数应该是“3”,十位数字是“1”即“31”开头的四位数有 个;同理,以“36”、“37”、“38”开头的数也分别有12个,所以第114个数的前两位数必然是“39”,而“3 968”排在第6个位置上,所以“3 968” 是第114个数.
个;同理,以“36”、“37”、“38”开头的数也分别有12个,所以第114个数的前两位数必然是“39”,而“3 968”排在第6个位置上,所以“3 968” 是第114个数.
⑵ 由上可知“37”开头的数的前面有60+12+12=84个,而3 796在“37”开头的四位数中排在第11个(倒数第二个),故3 796是第95个数.
示例五: 用0,1,2,3,4,5组成无重复数字的四位数,其中
⑴ 能被25整除的数有多少个?
⑵ 十位数字比个位数字大的有多少个?
解: ⑴ 能被25整除的四位数的末两位只能为25,50两种,末尾为50的四位数有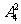 个,末尾为25的有
个,末尾为25的有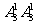 个,所以一共有
个,所以一共有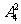 +
+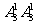 =21个.
=21个.
注: 能被25整除的四位数的末两位只能为25,50,75,00四种情况.
⑵
用0,1,2,3,4,5组成无重复数字的四位数,一共有 个.因为在这300个数中,十位数字与个位数字的大小关系是“等可能的”,所以十位数字比个位数字大的有
个.因为在这300个数中,十位数字与个位数字的大小关系是“等可能的”,所以十位数字比个位数字大的有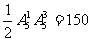 个.
个.
3.分类、分布思想的应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com