
17. 从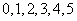 中任取3个数字,组成没有重复数字的三位数,其中能被5整除的三位数共有
个。(用数字作答)
中任取3个数字,组成没有重复数字的三位数,其中能被5整除的三位数共有
个。(用数字作答)
16. 同时抛掷两枚相同的均匀硬币,随机变量ξ=1表示结果中有正面向上, ξ=0表示结果中没有正面向上,则Eξ= .
15. 某班委由4名男生和3名女生组成,现从中选出2人担任正副班长。其中至少有一名女生当选的概率是 。(用分数作答)
14. 某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为80人,则n= .
13. 从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有( )
A.210种 B.420种 C.630种 D.840种
12. 有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是( )
A.234 B.346 C.350 D.363
11. 甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是p2,那么恰好有1人解决这个问题的概率是了( )
A.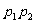 B.
B.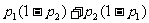
C.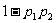 D.
D.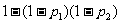
10. 某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为:( )
A.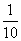 B.
B.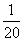 C.
C.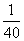 D.
D.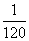
9. 已知盒中装有3只螺口与7只卡口灯炮,这些灯炮的外形与功率都相同且灯口向下放着,现需要一只卡口灯炮使用,电工师傅每次从中任取一只并不放回,则他直到第3次才取得卡口灯炮的概率为( )
A.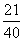 B.
B.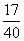 C.
C.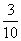 D.
D.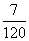
8. 将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法种数为( )
A.120 B.240 C.360 D.720
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com